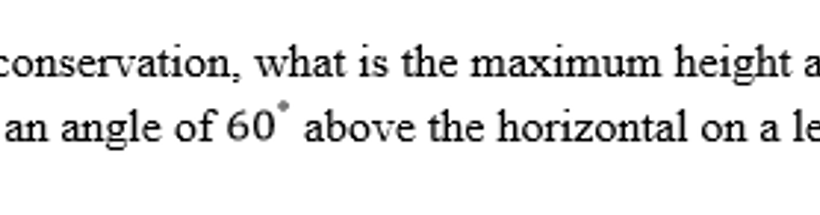Have you ever pondered the heights one can reach with the aid of mechanical energy? Imagine launching a projectile into the sky, only to wonder how high it can ascend. The relationship between mechanical energy and maximum height is not only fascinating but also steeped in the principles of physics. We will explore this connection thoroughly, unraveling the mysteries of energy conservation and the calculations necessary to determine maximum height.
In physics, mechanical energy is the sum of potential energy and kinetic energy. When an object is propelled upwards, it experiences a transformation of energy that can be described using the conservation of mechanical energy principle. This principle states that in an ideal scenario—meaning no energy is lost to air resistance or friction—the total mechanical energy of the system remains constant. As an object ascends, its kinetic energy, which is energy in motion, is converted into potential energy, the energy of position. When the object reaches its highest point, its kinetic energy is at a minimum, while its potential energy is at a maximum.
To illustrate this concept, consider a simple scenario: a ball thrown upward. The initial kinetic energy of the ball can be expressed by the equation:
K.E. = 1/2 mv²
where m is the mass of the ball and v is its initial velocity. As the ball rises, it slows down due to the force of gravity acting against it, converting its kinetic energy into gravitational potential energy, represented by:
P.E. = mgh
In this equation, h represents the height attained above the ground level, and g is the acceleration due to gravity (approximately 9.81 m/s² on Earth). At the highest point of the ball’s trajectory, the mechanical energy is conserved, so:
K.E. initial = P.E. maximum
This relationship can be mathematically expressed as follows:
1/2 mv² = mgh
From this equation, we can isolate h to find the maximum height:
h = v² / (2g)
This equation is both elegant and powerful. It demonstrates that if you know the initial velocity of an object, you can calculate the maximum height it will reach as long as air resistance is negligible. However, let us delve deeper to explore how variations in initial velocity influence the height. Increasing the speed at which the ball is launched will exponentially increase the height attained. This relationship is quadratic in nature since height increases with the square of velocity. For instance, if you double the initial speed, the height achieved will quadruple. Isn’t that a remarkable insight into the dynamics of energy and motion?
Now, let’s address a potential challenge. In real-world situations, air resistance plays a significant role in the performance of the projectile. The heavier and more streamlined an object is, the less it will be affected by drag forces. This means that experiments involving lighter or less aerodynamic objects may yield heights that fail to conform to the theoretical predictions of the equations presented above. The implications of this deviation open a plethora of topics worth discussing, including advanced modeling of drag forces and the impacts of varying atmospheric conditions on projectile motion.
To mitigate the effects of air resistance, one can conduct experiments in controlled environments. Using vacuum tubes can effectively eliminate drag forces, allowing for a clearer observation of the relationship between mechanical energy and maximum height. However, in everyday scenarios, understanding and approximating the effects of air resistance may still retain significance for more accurate predictions.
The intricacies of mechanical energy conservation not only apply to simple projectile motion but also find relevance in varied fields such as sports, engineering, and environmental sciences. For instance, understanding the mechanical energy principles behind climbing sports can contribute to developing superior training methods that enhance athletes’ performance and efficiency.
Moreover, in the environmental context, analyzing energy conservation helps in designing eco-friendly transportation systems. For every vehicle or projectile launched into the air, adaptive engineering can minimize energy waste, ultimately leading to greener solutions that emphasize energy sustainability. Such advancements can inspire innovations in renewable energy technology, showcasing the real-world significance of these mechanical concepts.
As we embrace the lessons of mechanical energy conservation and its applications, we can appreciate how the understanding of height, motion, and energy converges. Engaging with practical problems and challenges encourages deeper comprehension of the scientific principles governing our world. Thus, when next confronted with the mystery of how high something can fly or rise, remember that the answers lie in the fascinating interplay of mechanical energies, fundamentally rooted in the laws of physics.
In conclusion, mechanical energy provides an accessible pathway to determine maximum height systematically. By mastering the equations and developing an understanding of the impact of variables such as initial velocity and air resistance, one can unveil the mathematical beauty behind the ascent of objects. Whether it’s a ball thrown in the air or engineers designing vehicles, the underlying principles of energy conservation continuously illuminate the potential heights we can reach—both literally and metaphorically.