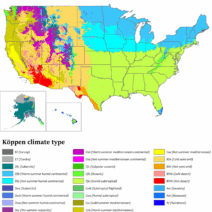
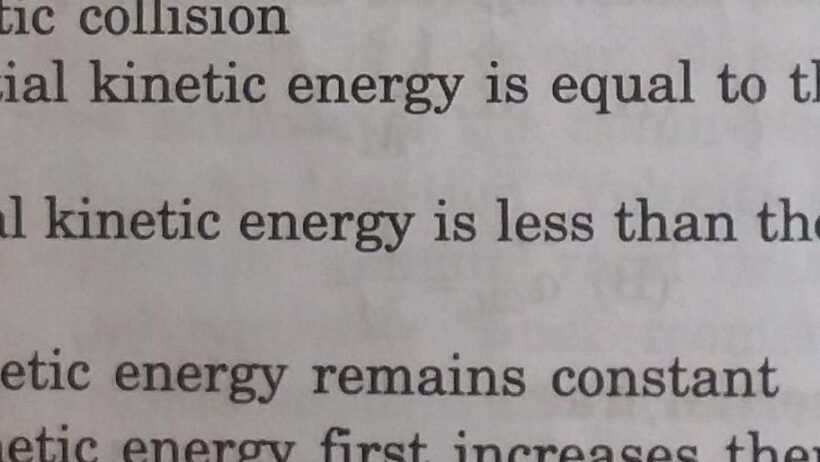When contemplating the natural laws governing motion and interaction, one might metaphorically liken the principles of perfectly elastic collisions to a dance—fluid, rhythmic, and defined by an unyielding adherence to structure. In this intricate ballet of particles, one fundamental question arises: Do perfectly elastic collisions always conserve kinetic energy? To comprehend this, one must delve deeper into the nuances of physical interactions, the definitions that frame them, and the constants that govern their behavior.
At the outset, it is essential to define the term “perfectly elastic collision.” These collisions occur when two bodies collide and, upon separation, the total kinetic energy remains unchanged. Analogous to two dancers who, after a collaborative twirl, return to their original positions without losing momentum, perfectly elastic collisions showcase an idealized state of energy conservation. Notably, in reality, such conditions are rare; however, they serve as a valuable model in physics.
The cornerstone of this concept is that in a closed or isolated system, where no external forces act upon the colliding bodies, the total momentum and kinetic energy are conserved. This is akin to a cosmic equilibrium—a celestial balance where the energy flows seamlessly between participants, never dissipating, and remaining eternally intact.
However, to understand the scope of energy conservation in these collisions, it becomes necessary to explore the underlying mechanics. Newton’s laws provide the framework within which these collisions operate. The first law, which states that an object in motion will remain in motion unless acted upon by an external force, illustrates how momentum can shift during interactions. In perfectly elastic collisions, both conservation laws—momentum and kinetic energy—are satisfied, ensuring that neither dancer falters in their step or loses energy to entropy.
Consider the mathematical expressions governing these interactions. The equation for kinetic energy is represented as K = ½ mv², wherein m signifies mass and v depicts velocity. In the instance of a perfectly elastic collision, the sum of the kinetic energies before impact equals the sum of kth energies post-impact. Mathematically, this can be delineated as:
K1 + K2 = K1′ + K2′,
where K1 and K2 are the kinetic energies of the two colliding bodies before, and K1′ and K2′ are their kinetic energies after the collision.
Nevertheless, bringing a metaphorical lens to this examination, while perfectly elastic collisions behave like a harmonious duet, the reality of physical interactions often resembles a cacophony of different musical styles, where collisions might not retain their original resonance. In most real-world applications, elastic collisions exist on a spectrum, and thus, the term “perfectly elastic” remains somewhat of a misnomer. When examining instances of collisions, friction, sound production, and deformation often intervene, robbing the kinetic energy from the pristine equations that define ‘perfection’.
To elucidate this concept, consider an everyday example—bouncing a basketball. When the ball strikes the ground, we anticipate an energetic rebound. However, it does not return to its original height due to energy loss through heat generated during impact and sound produced when it hits the floor. These losses illustrate a common deviation from perfect elasticity. Therefore, while the total momentum might be conserved, the kinetic energy is compromised, veering away from the ideal paved by theoretical physics.
A stark discrepancy emerges in scenarios involving perfectly inelastic collisions, where the colliding objects stick together post-impact. This scenario blurs the lines of energy conservation as kinetic energy is disbursed as internal energy, sound, or even thermal energy. The aftermath visually echoes a grip of entrapment—dancers now entangled, fluidity disrupted, seizing mobility and employing their kinetic energy unwittingly into other forms, ultimately losing the clarity of their initial vibrancy.
Moreover, one may ponder the implications of these collisions on macroscopic phenomena. Take cosmic bodies such as asteroids or comets veering towards one another—some may collide elastically, preserving their kinetic energy, while others, enmeshed by gravity, merge to form new celestial debris. The latter scenario evokes a poignant reminder: the universe thrives on transformation and adaptation, a dynamic interplay of energy that transcends mere conservation.
This leads us toward a philosophical consideration of conservation itself—an abiding principle that stands impervious in certain contexts while under constant challenge in others. In contemplating the balance between conservation and transformation, we uncover layers of understanding about energy’s destiny—whether it thrives unspent or evolves into transformed states, forever ebbed in an oscillating continuum.
In conclusion, while perfectly elastic collisions theoretically conserve kinetic energy, real-world interactions often betray this ideal, fragmented by the inefficiencies of nature. The dance of particles evokes an exquisite balance, yet one must not overlook the nuances of their interactions. Understanding the ebb and flow of conservation within perfectly elastic collisions deepens our appreciation for the elegant principles that underpin the universe—and encourages an ongoing dialogue about the fragile balance between conservation and transformation in an ever-evolving world.