Inelastic collisions present a fascinating paradox within the realms of physics, particularly in relation to energy conservation laws. To grasp the implications of such collisions, one must first delineate the fundamental principles guiding classical mechanics. The law of conservation of energy asserts that energy cannot be created or destroyed, but can only be transformed from one form to another, a principle that underpins nearly all physical interactions.
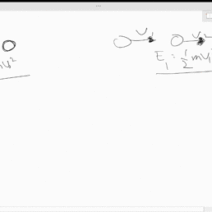
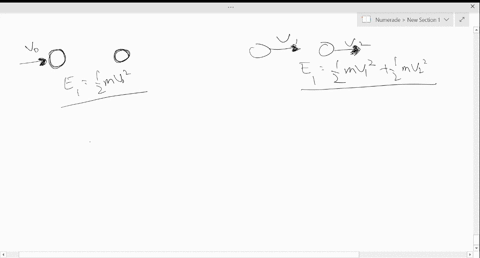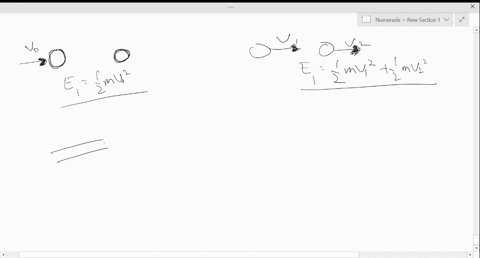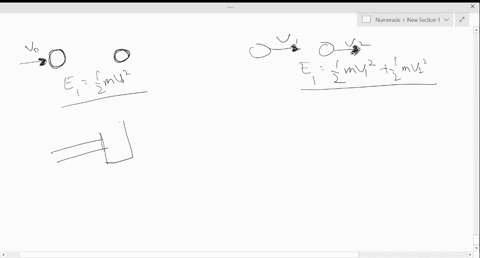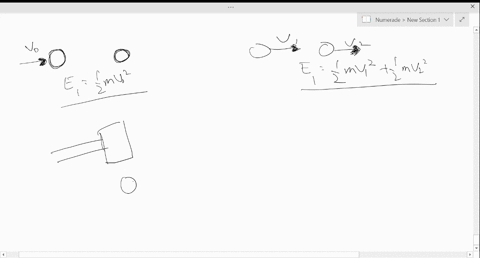
Collisions are broadly categorized into two types: elastic and inelastic. In an elastic collision, both kinetic energy and momentum are conserved; the objects involved rebound without any permanent deformation or generation of heat. Conversely, inelastic collisions, which are ubiquitous in everyday life, do not conserve kinetic energy, leading to a common misconception that they contravene the law of conservation of energy.
To understand why inelastic collisions adhere to energy conservation laws, it is essential to define what occurs during such interactions. In an inelastic collision, momentum is conserved while kinetic energy is not. The loss of kinetic energy typically converts into other forms of energy, such as heat, sound, and deformation. For instance, when two cars collide, some energy is absorbed by the crumpling of metal and transformed into sound, leaving the vehicles with reduced kinetic energy post-collision.
Consider the example of two clay balls colliding and sticking together. Upon impact, the initial kinetic energy is dissipated due to internal friction within the clay and sound produced during the collision. The stickiness of the clay illustrates how objects can coalesce, demonstrating a significant energy transformation rather than outright loss.
Further analysis reveals that the energy lost in an inelastic collision is not annihilated; it simply transitions into different forms. This aligns with the principle of conservation of energy, whereby the overall energy of a closed system remains constant, even if kinetic energy diminishes. It is a common mistake to equate the conservation of kinetic energy with the broader conservation of energy.
Considering the mathematical perspective enhances understanding. The total energy in a system comprising two colliding bodies can be constitutively expressed. For instance, in an elastic scenario, if two objects with masses m1 and m2 collide with velocities v1 and v2, the total kinetic energy before collision (KE_initial) equals the total kinetic energy after collision (KE_final). However, for inelastic collisions, KE_initial does not equal KE_final. The disparity accounts for the energy transformed into other forms.
Another concept worth exploring is the coefficient of restitution, which indicates how elastic a collision is. A coefficient of 1 indicates a perfectly elastic collision, while a coefficient of 0 signifies a perfectly inelastic collision where the two bodies stick together. This coefficient mathematically encapsulates how momentum and energy shift between forms during the collision process.
In examining real-world applications, inelastic collisions can be observed across various scenarios—from vehicle accidents to sports events—where objects interact. The implications of these interactions are not merely theoretical; they resonate in the engineering of safer vehicles and the design of sports equipment. An understanding of energy distribution during collisions informs the creation of crumple zones in cars that absorb impact, thereby minimizing injuries.
Furthermore, inelastic collisions also play a crucial role in systems that utilize energy transformations, such as hydraulic systems or industrial machinery, where energy losses due to friction and heat are an integral aspect of their efficiency and design. Recognizing that energy conversion is inherent to these systems further underscores the importance of comprehending the dynamics of inelastic collisions.
Critically, inelastic collisions are not strictly limited to macroscopic phenomena. At the molecular level, inelastic scattering occurs when particles collide, leading to changes in their kinetic states. These interactions are pertinent in fields such as quantum mechanics and thermodynamics, underpinning principles that govern atomic and molecular behavior. The energy transitions occurring at this level illustrate that conservation laws extend beyond classical paradigms, retaining relevance in complex systems.
This discourse reverberates through the ongoing explorations in physics, prompting deeper inquiries into the nature of energy and its conservation in various contexts. With the advent of new technologies and methodologies in scientific research, understanding the intricacies of energy dynamics continues to evolve. The phenomena of inelastic collisions serve as a critical lens for validating fundamental laws, ensuring that the nexus of energy remains intact amidst transformations.
In conclusion, while inelastic collisions may appear to challenge the law of conservation of energy through their apparent loss of kinetic energy, a thorough examination elucidates that these interactions are consistent with the broader principle. Energy is neither lost nor destroyed; instead, it metamorphoses into various forms revealing complex interrelations within physical interactions. A comprehensive grasp of these concepts not only enriches our theoretical understanding but also arms us with the knowledge necessary to apply these principles in practical, real-world contexts. As such, the exploration of collisions, both elastic and inelastic, continues to be a vital domain within physics, shedding light on the intricate dance of energy in our universe.