The Work-Energy Theorem is a pivotal concept in classical mechanics, asserting that the work done on an object is equal to the change in its kinetic energy. This theorem is often illustrated in contexts involving conservative forces, such as gravity and spring forces, which have unique characteristics. However, the question arises: does the Work-Energy Theorem solely apply to conservative forces? The exploration of this query not only delves into the theorem’s fundamental principles but also challenges conventional thought that may limit its application.
To unpack the implications of this question, it is essential to distinguish between conservative and non-conservative forces. Conservative forces are path-independent, meaning the work done by these forces only depends on the initial and final positions of the object, not on the trajectory taken. For instance, gravitational force and spring force are quintessential examples. When an object falls under the influence of gravity, the work done is solely a function of its height difference, and energy is conserved in the system.
On the other hand, non-conservative forces, such as friction and air resistance, exhibit path dependence. The work done by these forces is contingent upon the specific path taken and results in energy dissipation, typically transformed into thermal energy. This introduces a layer of complexity when applying the Work-Energy Theorem. Despite these differences, the theorem can be extended beyond the realm of conservative forces.
When friction acts on a moving object, for instance, it opposes the motion, resulting in a net reduction in kinetic energy. This challenge brings to light an imperative aspect: while the theorem originally suggests a straightforward relationship between work and kinetic energy, the realities of non-conservative forces necessitate a broader view. Thus, the theorem can be adapted to include a work term for non-conservative forces.
Mathematically, the Work-Energy Theorem can be expressed as:
W = ΔKE = KE_final - KE_initial
However, in the presence of non-conservative forces, this formulation must accommodate for the work done against such forces. The modified expression can be understood as:
W_total = W_conservative + W_non-conservative
This formulation highlights that the total work done encompasses both conservative and non-conservative elements. It posits that even when non-conservative forces are at play, one can still apply the Work-Energy Theorem by accounting for the additional energy transformations and losses involved in the system.
Furthermore, the implications extend to real-world phenomena where non-conservative forces are common. Consider the automotive industry, where engineers grapple with the omnipresent friction between tires and the road. The design of vehicles involves meticulous calculations to optimize performance, acknowledging that kinetic energy is not merely a function of acceleration but also a reflection of energy lost to non-conservative forces. Fuel efficiency, speed, and handling characteristics are integral to such designs, illustrating the theorem’s relevance in practical applications.
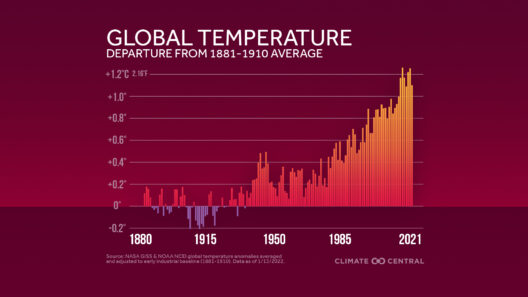
From a broader perspective, the adaptability of the Work-Energy Theorem to include non-conservative forces is akin to understanding the interconnectedness of environmental systems. Just as energy transformations within mechanics must be comprehended holistically, so too must the intricacies of climate systems be addressed. In climate science, acknowledging the numerous interactions between various forces—both natural and anthropogenic—is crucial too. The dissipative forces at play in our climate system require a nuanced understanding, similar to that of non-conservative forces in mechanics.
Moreover, one may pose a thought-provoking question: if we consider the historical evolution of the Work-Energy Theorem, could it not be paralleled with ongoing advancements in our comprehension of both mechanics and climate dynamics? Just as scientists refine their interpretations of physical laws, so too must society evolve in its approach to addressing climate change, leveraging multifaceted strategies that embrace both conservation and transformation of energy.
Ultimately, the assertion that the Work-Energy Theorem is limited to conservative forces proves to be a challenge when we consider practical applications and broader scientific principles. This nuanced understanding emphasizes that while conservative forces offer a simplification of energy dynamics, reality is often more complex. The theorem’s applicability extends into diverse realms, prompting a reassessment of doctrines that may inhibit critical innovation.
In summary, the Work-Energy Theorem does not apply exclusively to conservative forces. Through the lens of non-conservative forces, one can derive deeper insights into the nature of work and energy. This versatility underscores the importance of a holistic perspective, whether in mechanics or environmental science, as we navigate the intricate web of interactions that govern natural phenomena—the harmony between work performed and energy conserved remains a fundamental principle, irrespective of the forces involved.