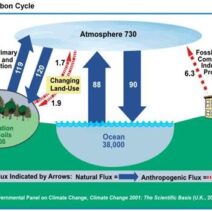
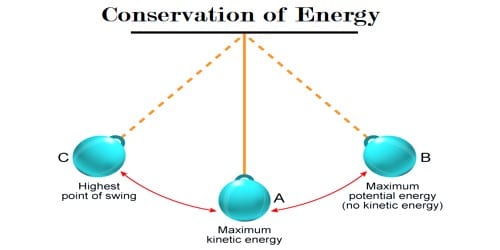
The simple pendulum is a captivating demonstration of fundamental principles in physics, particularly the conservation of energy. This classical mechanism consists of a weight, or bob, attached to a string of negligible mass suspended from a fixed point. As the bob swings back and forth, it provides an elegant illustration of how energy transforms rather than dissipates within a closed system. Understanding this transformation not only sheds light on pendular motion but also underscores the broader principles of energy conservation relevant to various systems in nature.
To begin, it is essential to delineate the components at play in a simple pendulum. The gravitational force acting on the pendulum is the key player in its motion. As the bob is released from a certain height, it possesses gravitational potential energy, determined by the height from which it descends. This potential energy can be quantified using the formula: (PE = mgh), where (m) represents mass, (g) is the acceleration due to gravity, and (h) is the height relative to a given reference point.
Upon release, the bob begins its descent, and the gravitational potential energy is converted into kinetic energy, defined as the energy of motion. The kinetic energy can be expressed mathematically as (KE = frac{1}{2}mv^2), with (m) as the mass and (v) as the velocity of the bob. At the lowest point of the swing, all the gravitational potential energy has been transformed into kinetic energy, resulting in the maximum velocity of the bob. This interplay between potential and kinetic energy exemplifies the principle of energy conservation.
As the pendulum ascends to its opposite extreme, the process reverses. The kinetic energy decreases as the bob slows down, while the gravitational potential energy increases due to the height again. It is noteworthy that during this oscillatory motion, the total mechanical energy of the system—comprising both potential and kinetic energy—remains constant, barring external forces such as air resistance or friction at the pivot. This phenomenon encapsulates the ethereal beauty of energy conservation, providing an intuitive visual representation of what may initially appear to be abstract scientific principles.
A salient observation regarding the simple pendulum is its ability to reach a state of periodic motion. The bob oscillates in a predictable manner, completing cycles that maintain identical duration and amplitude given undisrupted conditions. This regularity raises questions about the underlying reasons for such behavior. The uniformity of the gravitational field appears to constrain the movement, and the elastic properties of the string transmute forces efficiently, allowing unimpeded energy transfer. These factors coalesce to create an unbroken loop of energy transformation, where mechanical energy flows seamlessly between potential and kinetic forms.
A deeper exploration of the conservation of energy within the context of a simple pendulum also unveils critical implications for broader environmental contexts. For instance, energy conservation principles permeate ecological systems, wherein energy from the sun is captured by plants through photosynthesis and subsequently transferred through the food web. The closed loop of energy transfer can be likened to the cyclical nature of a pendulum, supporting life in myriad forms while underscoring the necessity of maintaining equilibrium within ecosystems.
Furthermore, the phenomenon of damping, a process whereby energy dissipates over time due to non-conservative forces such as air resistance and friction, introduces a layer of complexity to the idealized model of a simple pendulum. As the pendulum swings, energy loss leads to a gradual decrease in amplitude, thereby illustrating how, in real-world systems, conservation is often imperfect. This observational nuance emphasizes the importance of minimizing energy loss in societal applications, prompting innovations in fields like renewable energy, where efforts are directed towards efficient energy transfer and storage.
Investigating the simple pendulum also affords an appreciation for the historical advancements in the understanding of energy conservation. Figures such as Galileo and Newton laid the groundwork for classical mechanics, enhancing our comprehension of motion and energy transfer. The pendulum, often associated with the measurement of time, intertwines physics with practical applications, rendering it a tool for exploration and experimentation that has stood the test of time.
Perhaps the most enchanting aspect of a simple pendulum is its ability to manifest complex principles of physics through a straightforward yet mesmerizing motion. Observing the rhythmic swing can cultivate a sense of wonder as one acknowledges the intricate dance between potential and kinetic energy. It serves as a microcosm of larger natural phenomena, a reminder of the interconnectedness of energy systems, whether they be mechanical, ecological, or even cosmological.
In conclusion, the simple pendulum is more than a mere apparatus demonstrating basic physics; it is a profound illustration of the conservation of energy. Its cyclical movement encapsulates the elegance of energy transformations, while inviting deeper contemplation on the implications of this conservation in multifaceted environments. As society continues to grapple with challenges related to energy consumption and environmental stewardship, the simple pendulum serves as a timeless symbol of balance, harmony, and the enduring laws that govern our physical world.