Understanding the conservation of mechanical energy is a pivotal concept in physics that has profound implications across various domains, such as engineering, environmental science, and everyday life. The principle states that in a closed system, where only conservative forces act, the total mechanical energy remains constant over time. This foundational notion encompasses both potential energy and kinetic energy, offering insights into the behavior of objects in motion and the forces that influence them.
To calculate conservation of mechanical energy effectively, one must grasp the two primary forms of mechanical energy:
- Kinetic Energy (KE): This is the energy an object possesses due to its motion, calculated using the formula KE = ½ mv², where m denotes mass and v represents velocity.
- Potential Energy (PE): This is the energy stored in an object due to its position or configuration. The gravitational potential energy is commonly calculated as PE = mgh, where g is the acceleration due to gravity and h is the height above a reference point.
The usage of the aforementioned equations enables the establishment of a mathematical framework for calculating the conservation of mechanical energy. The total mechanical energy (TME) can be represented as:
TME = KE + PE
In ideal conditions, where no external forces like friction or air resistance are present, the total mechanical energy before any event will equal the total mechanical energy after said event. Thus, it is articulated as:
KE_initial + PE_initial = KE_final + PE_final
Let’s delve deeper into practical examples where this principle is exhibited.
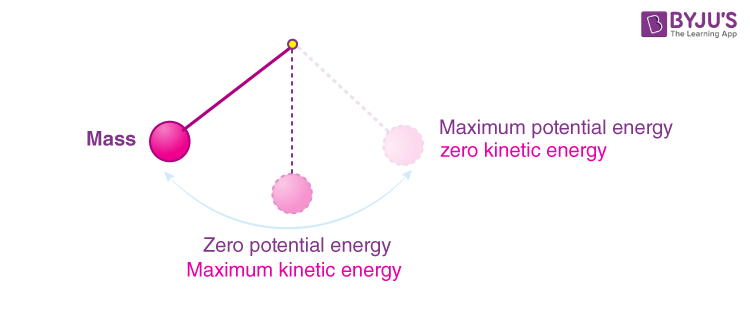
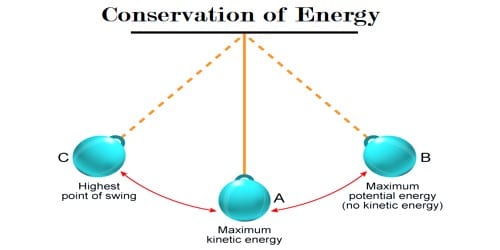
Example 1: A Pendulum’s Swing
Consider a simple pendulum comprising a mass (the bob) attached to a string. As the pendulum swings, energy conversion occurs between kinetic energy and potential energy. When the pendulum reaches its highest point, kinetic energy is at its minimum, while potential energy is at its maximum.
At the lowest point of the swing, kinetic energy peaks, and potential energy diminishes. By applying the conservation of mechanical energy equation:
PE_initial + KE_initial = PE_final + KE_finalOne can utilize measurable quantities like mass, height, and velocity to deduce energy transformations, perfectly illustrating how total energy remains conserved throughout the swing.
Example 2: Roller Coasters
Roller coasters provide a magnificent illustration of the conservation of mechanical energy concept. At the highest point of the coaster, the potential energy is maximized. As the coaster plunges downward, potential energy transforms into kinetic energy, increasing speed as it descends.
Calculating the energies at different heights can illustrate the interplay of forces in a real-world context. The formula can be applied to determine the speed at different points of the track, revealing how energy persists and shifts forms while remaining constant in totality.
Assessment of Energy Losses
In practical scenarios, energy losses due to non-conservative forces such as friction must be considered. This aspect of the conservation of mechanical energy principle acknowledges that real systems often experience energy dissipation. For instance, when analyzing a skydiver, while the potential energy decreases with altitude, kinetic energy increases. However, a portion of mechanical energy is transformed into thermal energy due to air resistance, which is a critical factor in such calculations.
Thus, the energy conservation equation adapts to account for energy losses:
TME_initial - Work_done_by_non-conservative_forces = TME_finalRecognizing and quantifying such losses, although complex, enhances the accuracy of energy predictions in various applications.
Implications in Various Fields
The ability to calculate and understand the conservation of mechanical energy has far-reaching implications. In engineering, it aids in designing efficient machines and systems, ensuring energy is not dissipated unnecessarily. In environmental science, understanding energy transfer can illuminate the sustainability of processes and systems, impacting energy conservation measures.
Performance in sports can also be improved through a deeper comprehension of mechanics. Athletes can optimize their motions, conserving energy more effectively during execution—illustrating how mechanical energy conservation extends beyond physics into biomechanics.
Conclusion
In essence, mastering the principles and calculations involved in the conservation of mechanical energy unlocks a treasure trove of knowledge that can be applied in myriad fields. By understanding energy transformations and the conditions for conservation, this principle fosters innovation and efficiency.
Through detailed calculations, real-world applications, and the consideration of energy losses, one can appreciate the intricacies of mechanical energy. The lens of conservation opens pathways to not only harness energy but to also advocate for a more sustainable future, respecting the delicate interplay of forces that govern our physical universe.