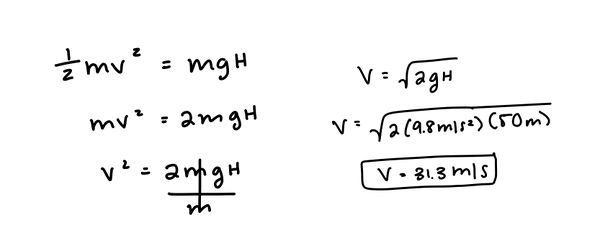Have you ever wondered how high a ball must be dropped to achieve a specific speed just before it strikes the ground? This question, while seemingly elementary, presents a fascinating challenge steeped in the laws of physics, particularly the conservation of energy. This principle states that in a closed system, the total energy remains constant, which means it can transform from one type to another, such as potential energy (PE) to kinetic energy (KE). Let’s delve into how to calculate the initial height from which an object must fall, using this foundational concept.
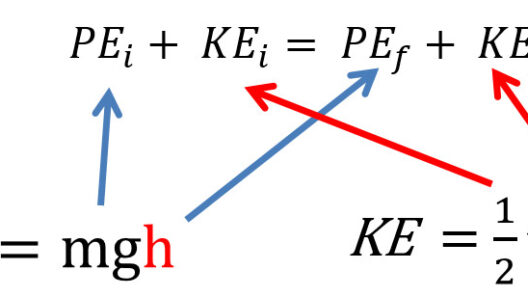
To begin, it’s crucial to understand the two types of mechanical energy involved: potential energy and kinetic energy. Potential energy is the energy stored in an object due to its position in a gravitational field, and it can be calculated by the equation:
PE = mgh
In this formula, m represents the mass of the object (in kilograms), g is the acceleration due to gravity (approximately 9.81 m/s² on Earth), and h is the height above the ground (in meters). When the object is released and falls, the potential energy is converted into kinetic energy, which is the energy of motion. The kinetic energy can be given by the formula:
KE = 0.5mv²
In this equation, v stands for the velocity of the object just before impact. As the object falls, the potential energy at height h transforms into kinetic energy when it reaches the ground.
Now, here comes the playful challenge: If we know the speed of the object just before it impacts the ground, how can we determine the height from which it was dropped? To discover the initial height, we must set the potential energy equal to the kinetic energy at the moment just before impact, as per the conservation of energy principle.
Mathematically, this can be expressed as:
mgh = 0.5mv²
Notice that the mass m appears in both terms. Consequently, it can be eliminated from the equation, leading us to:
gh = 0.5v²
Next, we can isolate h by rearranging the equation:
h = (0.5v²) / g
This formula now allows us to calculate the initial height if we input the speed just before impact (v) and the gravitational acceleration (g). For example, if an object strikes the ground at a speed of 20 m/s, you would substitute this value into the formula:
h = (0.5 * (20 m/s)²) / (9.81 m/s²)
Calculating further, we find:
h = (0.5 * 400) / 9.81
h ≈ 20.41 meters
This tells us that the object must have been dropped from a height of approximately 20.41 meters for it to hit the ground at a speed of 20 m/s. It’s quite captivating to see how such simple principles can help us comprehend the relationship between different forms of energy.
When applying this principle, we must also consider a few practical aspects. The conservation of energy in a real-world scenario may be influenced by factors such as air resistance and friction, which can impede the energy transfer process. Although this is an idealized calculation that presumes a frictionless environment, it provides a useful approximation for understanding motion.
Moreover, this method of calculating height has wide-ranging applications, from playground safety designs (to ensure that falls from heights are within safe limits) to engineering scenarios involving the design of roller coasters or amusement rides where precise measurements are crucial to safety and performance.
In summation, calculating the initial height using the conservation of energy principle is not only an intriguing exercise but a fundamental aspect of physics that encompasses our everyday experiences. The dance between potential energy and kinetic energy showcases the beauty and predictability of physical laws. Next time you witness an object in free fall, pause for a moment and ponder the height from which it descends. Nature’s harmony in energy conversion and mechanics is truly a marvel.
In conclusion, grasping how to calculate initial height through energy transformation processes not only enriches one’s understanding of physics but also offers valuable insights into the design and safety of various objects and structures in our world. It serves as a reminder of the interconnectedness of principles in science and the practical applications that arise from them.