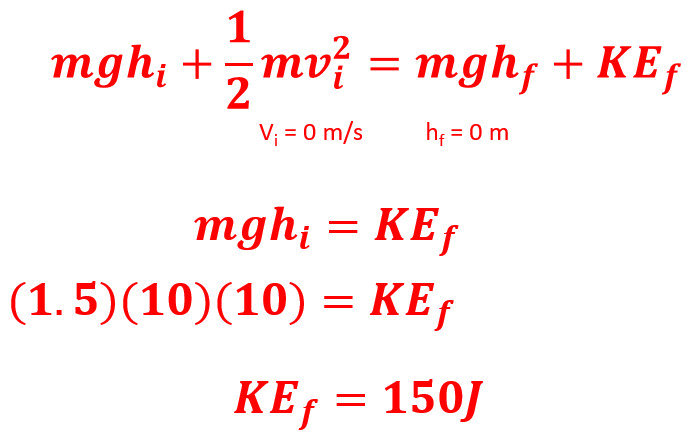Velocity calculations are central to understanding dynamics in physics, and the conservation of energy provides a profound method to determine these values. At first glance, the method may seem confined to theoretical applications, but its implications resonate with fascinating real-world phenomena. The principles involve not just mathematical prowess, but a kinship with the identical laws governing the natural world around us.
At its core, conservation of energy posits that energy cannot be created or destroyed; it can only be transformed from one form to another. This fundamental law of physics is emblematic of nature’s pursuit of balance and has far-reaching consequences across various branches of science and engineering.
To delve into the calculation of velocity using the conservation of energy, we first need to recognize the different forms of energy typically involved in mechanics: kinetic energy and potential energy. Kinetic energy (KE) is the energy an object possesses due to its motion, represented by the formula:
KE = 1/2 mv²
where m is the mass of the object and v is its velocity. Potential energy (PE), on the other hand, generally refers to gravitational potential energy when discussing objects near the Earth’s surface. Its formula is:
PE = mgh
Here, g represents the acceleration due to gravity (~9.81 m/s²), and h is the height above the reference point. When considering an object in free fall or any system where forces are in motion, such as a swinging pendulum or a rollercoaster, both kinetic and potential energy are at play.
The beauty of conservation of energy lies in its simplicity. For a system isolated from external forces, the total mechanical energy (sum of kinetic and potential energies) remains constant:
KE_initial + PE_initial = KE_final + PE_final
For example, envision a ball being dropped from a height. Initially, its potential energy is maximal, while kinetic energy is zero. As it descends, potential energy decreases, transforming into kinetic energy. At the moment before impact, potential energy is at its minimum, and kinetic energy reaches its peak. This transformation allows us to calculate the velocity just before impact.
Assuming we know the height from which the ball is dropped, the height h, we can set up the equation:
mgh = 1/2 mv²
Notice that mass m cancels from both sides, simplifying our work to:
gh = 1/2 v²
By rearranging this equation, we find:
v = √(2gh)
This formula elucidates how gravitational potential energy, via the height from which the ball is dropped, dictates its final velocity. It’s astounding how one can calculate the speed of a falling object solely based on its height—a tangible application of energy conservation.
One might ask why this method of calculating velocity is so universally applicable. The answer lies in its robust nature. Conservation laws are foundational principles that underpin various fields, from astronomy and engineering to environmental science. They highlight a consistent thread in the tapestry of physical laws—one that continues to inspire the pursuit of knowledge and greater understanding.
Moreover, the implications of understanding velocity through energy principles extend far beyond mere numbers. In environmental contexts, where we seek to harness energy efficiently—whether in designing efficient buildings, optimizing renewable energy systems, or mitigating the impacts of climate change—these calculations help elucidate performance and efficiency metrics. Energy efficiency translates to reduced emissions and a lesser environmental footprint.
Adopting this energy-based approach can scaffold momentum towards sustainability. For instance, take wind turbines: they convert kinetic energy from the wind into mechanical energy, which in turn can be transformed into electrical energy. Understanding velocity through conservation laws can aid engineers in maximizing this transformation, ensuring that every gust of wind contributes to the generation of clean energy.
In transport technology, where velocities dictate the effectiveness of fuel consumption and emissions, conservation principles can guide advancements in electric vehicles and alternative-fuel systems. By knowing the speeds associated with various system efficiencies, strides can be made toward innovations that lessen the reliance on fossil fuels.
Additionally, these same principles can be applied in the analysis of numerous environmental phenomena. For instance, the analysis of water flow in rivers—calculating velocities that lead to erosion, transport of sediments, and ecological impacts involves understanding the transformation of gravitational potential energy into kinetic energy.
The application of these principles exemplifies a fascinating continuum; understanding how energy interacts with velocity allows us to appreciate both natural occurrences and engineered systems. Whether in theoretical scenarios demonstrated in classrooms or practical applications in daily life, the intersection of physics and the environment reveals intricate and profound connections that merit exploration.
In conclusion, the velocity of an object can be calculated through the lens of conservation of energy, revealing magnificent truths about the natural world. This endeavor not only enhances our understanding of physics but also empowers us to create sustainable solutions in our pursuit of a balanced ecosystem. As we continue to grapple with the challenges posed by climate change, harnessing knowledge about energy transformation will be paramount in crafting a more equitable and environmentally conscious future.