Understanding how to find height using the principle of conservation of energy can unlock a new perspective on motion, potential energy, and the dynamics of physical systems. This principle asserts that energy cannot be created or destroyed, but merely transformed from one form to another. With this foundational concept in mind, we can delve deeply into the practical application of physics, particularly when it comes to calculating height in varied scenarios, such as free-fall or projectile motion.
To begin with, let’s establish the basic tenets of energy. Two principal forms of mechanical energy are central to our discussion: kinetic energy (KE) and potential energy (PE). Kinetic energy is the energy of motion, given by the formula:
KE = 1/2 mv²
Where “m” is mass and “v” is velocity. Conversely, potential energy, specifically gravitational potential energy (which is what we will focus on when assessing height) is expressed as:
PE = mgh
In this equation, “m” is mass, “g” is the acceleration due to gravity (approximately 9.81 m/s² on Earth), and “h” is the height above a reference point, usually the ground. The balance between kinetic and potential energy becomes pivotal in determining height.
### Step 1: Identify the System
When solving problems involving height, start by clearly defining the system you are examining. Are you dealing with a dropped object, a ball thrown upwards, or perhaps a roller coaster car? Each scenario invokes different considerations regarding energy transformation. Identifying whether energy is converted from potential to kinetic (as in falling objects) or from kinetic to potential (as in objects ascending) is critical.
### Step 2: Determine Initial and Final States
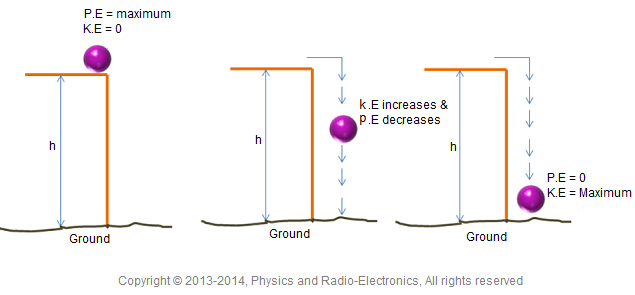
Next, examine the states of the system at two distinct points: the initial and the final state. For example, if a ball is thrown straight up, the initial state would be just as it leaves your hand, and the final state could be at the peak of its trajectory. The maximum height in this scenario is particularly interesting, as it represents a moment when kinetic energy reaches its nadir and potential energy crescendos.
### Step 3: Apply Conservation of Energy
Now, apply the conservation of energy principle. This principle posits that the total mechanical energy (the sum of kinetic and potential energy) must remain constant when only conservative forces are acting (i.e., neglecting air resistance and friction). Write the equation as follows:
KE_initial + PE_initial = KE_final + PE_final
Substituting in for the knowns according to your defined states will lead you to a configuration where you can solve for the unknown height “h.”
### Step 4: Use Specific Examples
Let us take a pragmatic example to illustrate this process. Suppose a ball of mass 2 kg is thrown upwards with an initial velocity of 10 m/s. We need to find the maximum height it reaches.
1. Calculate the initial kinetic energy:
KE_initial = 1/2 mv² = 1/2 (2 kg)(10 m/s)² = 100 J
2. At the peak height, the kinetic energy will be zero (KE_final = 0), and we are solving for height (h) where potential energy takes over:
PE_final = mgh = (2 kg)(9.81 m/s²)h
3. According to the conservation of energy:
KE_initial = PE_final → 100 J = (2 kg)(9.81 m/s²)h
Solve for “h”:
h = 100 J / (2 kg * 9.81 m/s²) ≈ 5.10 meters
This succinctly demonstrates how energy shifts form, culminating in our desired altitude.
### Step 5: Addressing Real-World Applications
From the macroscopic motions of roller coasters to the subtle nuances of how a tree absorbs sunlight, conservation of energy principles are paramount. Understanding height in such contexts is not merely mathematical; it is foundational to innovations in sustainable technologies, such as wind turbines and hydroelectric power systems, where elevation changes translate directly into energy capture.
When harnessing these principles, the importance of accuracy in measurement and calculation cannot be overstated. Factors such as air resistance and mechanical friction can introduce variances that obscure pure theoretical predictions. Thus, acknowledging these nuances fosters a deeper comprehension of energy dynamics in authentic scenarios.
### Step 6: Broader Implications in Physics and Beyond
By mastering how to derive height through conservation of energy principles, one cultivates a framework applicable across multiple disciplines. Not only does this knowledge support endeavors in engineering and mechanics, but it also bridges to ecological concerns, prompting considerations regarding energy conservation, sustainability, and the importance of clean alternative energy sources.
In conclusion, calculating height using the conservation of energy principle combines fundamental physics with practical applications that ripple through various fields. It compels individuals to appreciate the interconnectedness of energy forms and their real-world ramifications. By engaging with these concepts, one cultivates not only educational insights but also a broader awareness of energy’s role in the natural world.