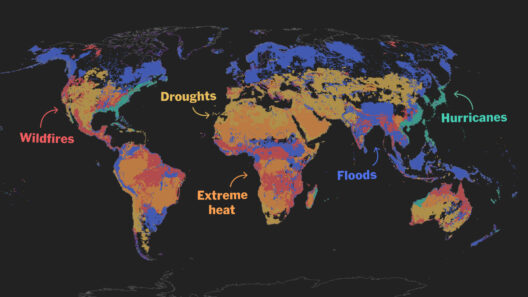
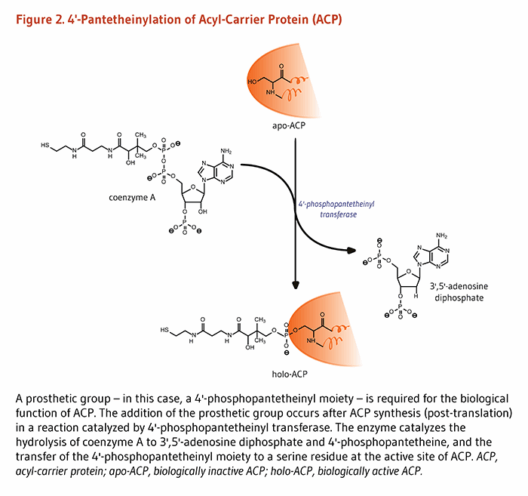
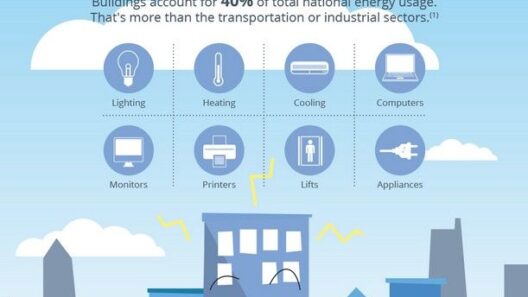
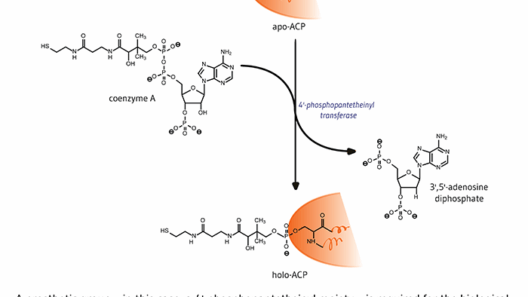
In the realm of physics, the principle of conservation of energy serves as a fundamental tenet, governing the interplay between various forms of energy. This principle asserts that energy cannot be created or destroyed, only transformed from one form to another. This characteristic is especially pivotal within mechanics, where the conversion between kinetic and potential energy underlies many phenomena. Understanding how to leverage the conservation of energy to deduce speed can be immensely beneficial in various applications, from basic physics problems to advanced engineering designs. This guide delves into the methodologies employed to find speed through the lens of energy conservation, furnishing readers with essential tips for quick calculations.
To commence, it is paramount to grasp the relationship between kinetic energy (KE) and potential energy (PE). Kinetic energy can be defined as the energy an object possesses due to its motion, mathematically represented as:
KE = ½ mv²
where m denotes mass, and v represents speed. Conversely, potential energy, particularly gravitational potential energy, is expressed as:
PE = mgh
Here, g signifies the acceleration due to gravity, and h is the height above a reference point.
At the heart of employing the conservation of energy to calculate speed lies the equality of total mechanical energy at two different points within a closed system. This iteration can often be summed up as:
KE_initial + PE_initial = KE_final + PE_final
This equation delineates that the total energy remains constant. By manipulating this equation, one can derive expressions to find speed given prevailing conditions.
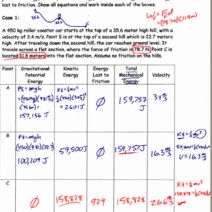
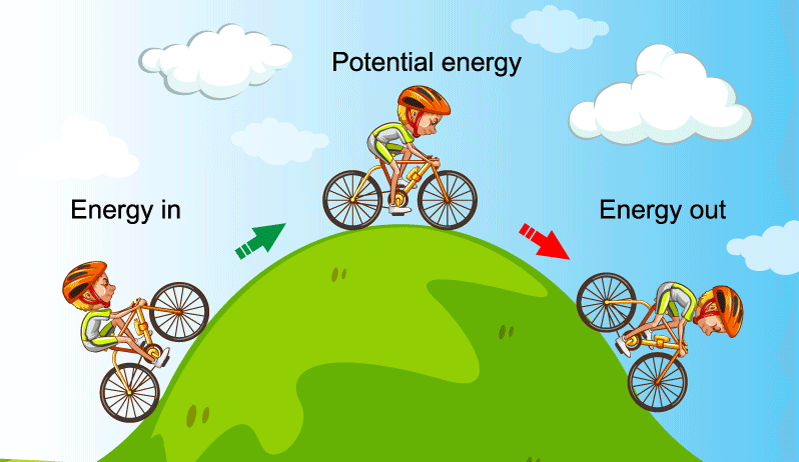
For instance, consider a scenario where an object is released from a height h. At the peak, it possesses potential energy but no kinetic energy because it is stationary. As it descends, potential energy is transformed into kinetic energy. By applying the conservation principle, one can determine the speed just before impact. Setting the initial potential energy equal to the kinetic energy at the lowest point provides clarity:
mgh = ½ mv²
Upon simplifying, the mass m cancels out from both sides, leading to the equation:
v = √(2gh)
This formula enables quick calculations of speed given height and gravitational acceleration, illustrating how quickly one can ascertain speed when armed with the fundamental principles of energy conservation.
In practical applications, varying factors may influence the outcome, necessitating additional considerations. For example, air resistance, friction, or other forms of energy dissipation may play a significant role, particularly in cases involving larger distances or higher velocities. When these elements are present, one must amend traditional calculative approaches to include energy losses, introducing complexities into the calculations.
Similarly, the conservation of energy principle can be employed in rotational motion, where the interplay between translational and rotational kinetic energy emerges. Rotational kinetic energy is articulated as:
KE_rotational = ½ Iω²
In this expression, I indicates the moment of inertia, and ω symbolizes angular velocity. Should one wish to connect linear speed to angular speed, the following relationship is pivotal:
v = rω
Integrating these ideas creates a framework through which one can also analyze wheels, discs, or any circular objects in motion. Determining rotational speeds involves pitfalls similar to linear dynamics. If energy conversion is understood clearly, finding speed in these contexts becomes straightforward and systematic.
In circumstances wherein potential energy is transformed into other forms aside from kinetic energy—like thermal energy—one must utilize a different approach. Situations characterized by non-conservative forces often require an analysis of work-energy principles wherein energy losses through friction or air resistance are accounted for, facilitated by the work-energy theorem:
Work = ΔKE
This theorem elucidates how work done on an object correlates with changes in kinetic energy, enabling musicians to compute the work done against resistive forces to ultimately find speed. In essence, the work performed alters the amount of mechanical energy available to an object.
Engaging further with this principle invites exploration into real-life contexts. For instance, roller coasters encapsulate conservation of energy splendidly; they ascend to elevated heights before plummeting, their kinetic energy peaking at the nadir. By employing conservation principles, engineers can foresee speeds at differing trajectories. Employing these principles effectively informs design constraints, enhancing safety and optimizing thrill.
Ultimately, the versatility of the conservation of energy principle in finding speed transcends mere academic inquiry. It is a cornerstone fostering innovation and analytical rigor in fields such as aerospace engineering, materials science, and environmental technology. From understanding the behavior of moving objects to optimizing systems for energy efficiency, the implications are ubiquitous.
In summation, mastering the methods of calculating speed through conservation of energy is not merely an academic exercise; it is a skill of considerable utility. Aspects such as the interplay between kinetic and potential energy, adjustments for non-conservative forces, and dynamic applications all contribute to a robust understanding that transcends theoretical boundaries. With practice, these calculation techniques can yield quick and precise answers, empowering students, educators, and professionals alike to navigate the complex landscape of physics with confidence.