The conservation of energy is a fundamental principle in physics that encapsulates the idea that energy within a closed system remains constant, merely transforming from one form to another. The fascinating case of a pendulum serves as a quintessential example of this principle, allowing us to explore energy transformations that occur in a cyclical motion. Observing a pendulum swinging back and forth can ignite curiosity about the forces at play and the underlying laws of physics governing its behavior.
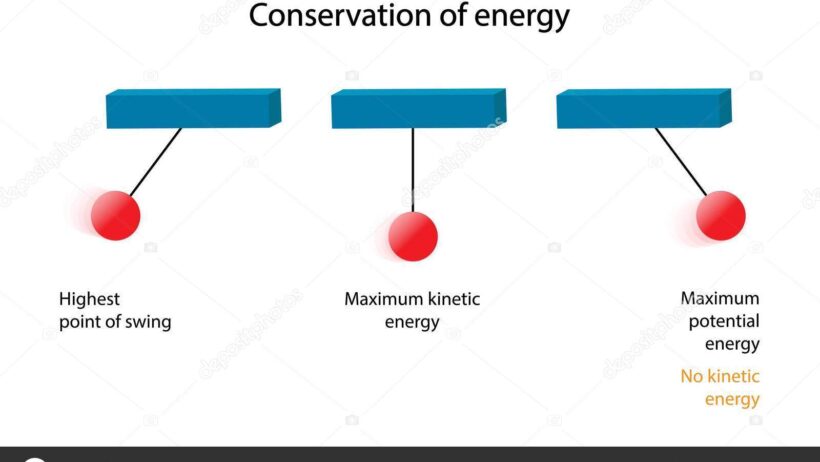
To delve into the conservation of energy in the context of a pendulum, we first establish the conditions necessary for a theoretical model. A simple pendulum consists of a mass, known as the bob, attached to a string or rod of negligible mass, pivoted at the upper end. When displaced from its resting position and released, the pendulum oscillates, converting potential energy into kinetic energy and vice versa. It is this transformation that is critical in proving the conservation of energy.
Initially, when the pendulum is at its highest point, it possesses maximum potential energy, defined by the height above the datum reference level. As it swings downwards, this potential energy is converted into kinetic energy—the energy of motion—as it reaches the lowest point of its swing. At this juncture, the kinetic energy is at its zenith, while potential energy dwindles to zero. The pendulum then ascends to the opposite height, once again converting kinetic energy back into potential energy, thus completing one cycle of motion. This cyclical exchange is what makes the pendulum a striking demonstration of energy conservation.
The mathematical representation of energy in a pendulum can further elucidate this principle. The potential energy (PE) at the highest point is calculated using the formula:
PE = mgh
where m is the mass of the bob, g is the acceleration due to gravity, and h is the height above the lowest point. Conversely, the kinetic energy (KE) at the lowest point can be expressed as:
KE = 0.5mv²
Here, v denotes the velocity of the bob at its lowest point. According to the conservation of energy principle, the total mechanical energy (TME) during the pendulum’s motion remains constant, where:
TME = PE + KE
By setting the potential energy at the maximum height equal to the kinetic energy at the lowest point, one can derive a clear relationship that exemplifies energy conservation:
mgh = 0.5mv²
Upon simplification, this equation highlights the inherent connection between the height and the velocity of the bob. The implications extend beyond mere numbers; they provide insight into how energy morphs through various states within the confines of an isolated system.
Yet, as enticing as this interplay of energy seems, reality introduces variables that can complicate this ideal scenario. Real-world factors such as air resistance and friction at the pivot point lead to energy dissipation, primarily as thermal energy. In such cases, the total mechanical energy diminishes over time, yet energy adheres to the conservation law, merely transitioning into less usable forms. This introduces an avenue for deeper inquiry into energy loss mechanisms and understanding real versus ideal systems, cementing the pendulum’s role not only as an educational tool but also as a conduit for broader ecological discussions regarding energy conservation.
Fascination with pendulums also transcends the educational realm, intertwining with historical and philosophical narratives about motion and existence. The very ability of a pendulum to maintain rhythm turns it into a metaphor for time, oscillation bridging science and the abstract. As society grapples with climate change challenges, the dance of a pendulum may symbolize the constant oscillation of our energy use and its impact on the environment. Recognizing the balance of energy conservation could hold the key to sustainable practices aimed at mitigating human footprint.
Educators and physicists alike advocate for hands-on experimentation to further cement understanding. Creating a pendulum from ordinary materials—a weight, string, and a fixed point—can provide profound insight into the principles of conservation of energy. Modifications such as varying mass or string length can also yield observations grounded in empirical data, illustrating different kinetic and potential energy transformations. By engaging in these experiments, students not only learn about theoretical constructs but also develop analytical skills, fostering deep thinking around physical phenomena.
Moreover, technological advancements have paved the way for precision measurements using digital tools. Such devices allow for high-fidelity observations of pendulum motion, surpassing traditional methodologies. The data collected can serve as a real-time analysis of energy conservation, providing compelling visualizations that elucidate the nuances of velocity and energy transformation.
Ultimately, the pendulum exemplifies an intersection of physics, history, and environmental consciousness. While investigating the conservation of energy in pendulums yields intricate insights into motion and energy dynamics, it also calls forth reflections on societal energy practices. In an era where sustainability is paramount, understanding these principles provides a foundational perspective on energy conservation’s role in averting climate change. As reflections swing back and forth like the pendulum itself, one is reminded of the delicate balance between energy consumption and ecological stewardship.