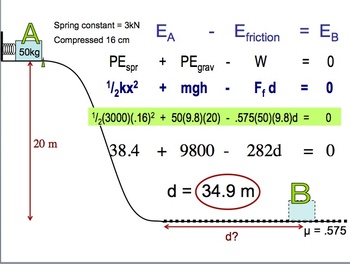
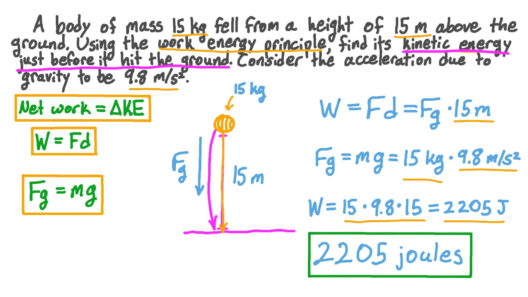
Understanding the conservation of energy is fundamental in both physics and real-world applications, particularly in addressing our urgent environmental challenges. By comprehending the principles underlying energy conservation, we can develop innovative solutions that contribute to a sustainable future. This guide seeks to kindle your curiosity, unveil the intricacies of energy conservation problems, and empower you to proficiently solve them while contemplating the broader implications on climate change.
Energy conservation entails the idea that energy cannot be created or destroyed; it can only be transformed from one form to another. This principle can be applied to a myriad of systems, from simple mechanical constructs to complex ecological interactions. The ensuing steps delineate a methodical approach that will enable you to set up and solve conservation of energy problems effectively, providing a robust foundation for deeper exploration.
Step 1: Grasp the Basic Concepts
Before diving into problem-solving, it is essential to familiarize yourself with the foundational concepts of energy. Energy exists in multiple forms, including kinetic energy (energy of motion), potential energy (stored energy based on position), thermal energy, and more. In typical conservation problems, the focus often rests on kinetic and potential energy.
For instance, potential energy can be calculated with the formula:
PE = mgh
Where:
PE= Potential Energym= massg= acceleration due to gravity (approximately 9.81 m/s²)h= height above a reference point
Kinetic energy is computed using the equation:
KE = 0.5 mv²
Where:
KE= Kinetic Energym= massv= velocity
These basic calculations will serve as the backbone for further problem solving.
Step 2: Identify the System
To set up an energy conservation problem, you must first identify the system in question. What physical scenario are you analyzing? It might involve a roller coaster, a pendulum swing, or even a diver leaping off a platform. Clearly defining the boundaries of the system will help isolate the energy transformations occurring within it. Not only does this clarify which forms of energy to consider, but it also allows you to focus on external influencers like friction or air resistance which can obscure your initial calculations.
Step 3: Establish Initial and Final States
Next, you will need to determine the initial and final states of the system. What is the system’s energy when it begins, and what is its energy at the conclusion of the scenario? Often, questions will provide parameters such as initial heights, velocities, and masses, which are pivotal in calculating the total energy at these two pivotal states.
For example, if a ball is dropped from a height, its initial potential energy at that height will transform into kinetic energy as it falls. A clear delineation of these states allows for the setup of key equations later on.
Step 4: Apply the Conservation of Energy Principle
With your system defined and states established, you can now apply the conservation of energy principle. In its essence, the total energy in a closed system must remain constant. Thus, the sum of potential energy and kinetic energy at the initial state should equal the sum at the final state. This can be expressed mathematically as:
PE_initial + KE_initial = PE_final + KE_final
This equation serves as the fulcrum that balances your initial conditions against your conclusions. Each term needs to be carefully evaluated and calculated to ensure accuracy.
Step 5: Solve for the Unknowns
Now that you have established a framework, you can solve for the unknowns within your equation. If you need to calculate the height at which a pendulum swings or the final speed of a diver hitting the water, simply rearrange the equation and isolate the variable of interest.
Remember, sometimes there are multiple unknowns, and you may need to utilize additional equations or data provided in the problem, such as conservation laws or derivatives of potential energy equations. Engaging with the intricacies of these calculations can provide surprising insights into the interplay between different energy forms.
Step 6: Interpret Results in Context
After arriving at a solution, the final and perhaps most critical step involves interpreting your results in a broader context. What do your findings imply for ecological systems? How does energy conservation apply to renewable energy technologies or waste reduction strategies? Considering these questions can pave the way for innovative approaches and solutions directed toward mitigating climate change.
In energy conservation problems, the journey does not merely end with the numerical answers. Rather, think critically about how the energy equations illustrate fundamental truths about our world. Each calculation, abstraction, and theorem aligns with the broader narrative of sustainability and ecological equity. The energy transformations you study operate under the same principles that govern the natural systems we live in.
By following these methodical steps and contemplating their relevance, you are not only enhancing your problem-solving skills but also fostering an awareness of how such principles inform solutions to pressing environmental issues. The harmony inherent in the conservation of energy encapsulates a profound responsibility—to understand, innovate, and ultimately protect our planetary home.