When considering the mesmerizing dance of a pendulum, one cannot help but draw parallels to the oscillations of our planet’s sustainability efforts. Just as the pendulum sways between points of equilibrium, we too must navigate the intricate balance required to address energy conservation in our ecosystems. Understanding the conservation of energy in a pendulum system serves not only as an intriguing academic exercise but also as a metaphor for the global pursuit of a more sustainable future.
Let us embark on a detailed exploration of how to solve a pendulum conservation of energy problem. We begin with the foundation of the concept—the principle of energy conservation itself. The law posits that energy in a closed system remains constant, transitioning between potential and kinetic forms without any loss. This principle is quintessential for analyzing a pendulum, where gravitational force and motion continually interplay.
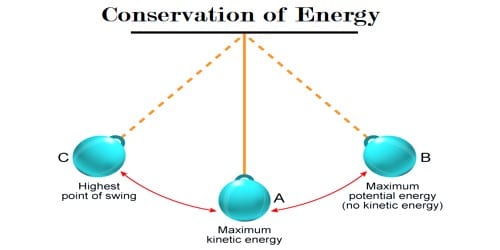
First, visualize the setup: a pendulum suspended from a pivot point, a mass (or bob) attached at the end of a string, ideally assumed to be massless and inextensible. When the pendulum is at rest in its lowest position, it possesses maximum kinetic energy yet no potential energy. Conversely, at the peak of its swing, where it defines its amplitude, the kinetic energy minimizes while potential energy peaks due to its height in the gravitational field.
To tackle a typical conservation of energy problem involving a pendulum, begin by delineating the heights involved. Let’s suppose the height (h) is determined by the displacement at the extreme position of the swing (its highest point). This height can be measured from the lowest point of the arc to the bob’s highest point.
The potential energy (PE) at the highest point can be calculated using the equation:
PE = mgh
Where:
- m = mass of the bob
- g = acceleration due to gravity (approximately 9.81 m/s²)
- h = height raised above the reference point
Equilibrium is maintained when energy transitions occur without friction or air resistance. Hence, as the bob swings downward, potential energy converts into kinetic energy (KE). At the lowest point, where the pendulum reaches maximum speed, kinetic energy takes the forefront:
KE = (frac{1}{2} mv^2)
Here, (v) represents the velocity of the pendulum at its nadir. As energy conservation dictates:
PE_initial = KE_max
This can translate into:
mgh = (frac{1}{2} mv^2)
Notice that the mass (m) cancels out, simplifying our equation into:
gh = (frac{1}{2} v^2)
From here, one can derive velocity (v) at the lowest point by rearranging the equation:
v = (sqrt{2gh})
The insights gleaned from this mathematical exploration not only highlight the beauty of the pendulum’s dynamics but also illuminate the concept of energy transformation—an essential component of any discourse on sustainability. In our efforts to combat climate change, the metaphor of the pendulum serves as a reminder to harness energy efficiently, transition towards renewable resources, and strive for an equilibrium that allows nature to flourish.
Exploring further, one can maneuver through various scenarios involving the pendulum. Consider adding friction or air resistance. Such external forces distort the idealized conservation of energy model. In a more realistic setting, energy would dissipate, manifesting as heat due to friction between the pendulum and the air, leading to gradual loss of amplitude over time. This scenario can be quantified, though it complicates the straightforward conservation equations. The lack of perfect efficiency reflects our own environmental challenges; while we strive for a sustainable future, various impediments, including socioeconomic factors and regulatory hurdles, often sap our momentum.
Moving forward, it is prudent to consider pendulums of varying lengths and masses. The period (T) of a simple pendulum, not defined by energy conservation but oscillatory behavior, is given by:
T = (2pisqrt{frac{L}{g}})
Where (L) is the length of the string. This formula highlights that the length of the pendulum greatly impacts its oscillation frequency but remains independent of mass. In contemplating climate solutions, different strategies and technologies may alleviate our carbon footprint; each with a unique impact yet bound by the overarching challenge shared across the globe.
Lastly, bringing these insights full circle encapsulates not only the equations and laws governing a pendulum but also the life lessons inherent in its mechanics. The pendulum vividly illustrates the necessity of balance—between energy consumption and conservation, between technological advancement and ecological preservation. As we endeavor to alter the trajectory of climate change, the elegant simplicity of a pendulum provides a framework through which we can view our progress and redefine our approaches to energy stewardship.
In conclusion, unraveling the intricacies of a pendulum’s conservation of energy is akin to a philosophical journey through the mechanics of our very existence on this planet. Both are about finding harmony—between forces, energy states, and ultimately, our approach to sustainability. Through such studies, we can foresee a world where equilibrium is achieved, not only in motion but in our response to the environmental crisis.