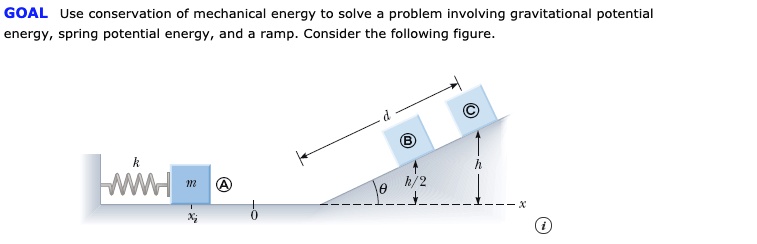
Understanding the intricate ballet of forces and energy in a spring system can often feel daunting. Yet, the principles of conservation of mechanical energy render this complexity manageable. By shifting your perspective and employing systematic strategies, you can master the mechanics of springs—whether you are grappling with a simple mass on a spring or delving into more elaborate oscillatory motions. Let’s embark on this enlightening journey through the realm of spring energy conservation. This exploration holds the promise of not only enhancing your analytical capabilities but also igniting your curiosity about the fundamental laws governing physical systems.
1. Grasping the Basics of Energy Types
Before tackling any spring conservation of energy problem, it’s imperative to comprehend the two primary forms of mechanical energy: kinetic energy (KE) and potential energy (PE). In the context of springs, elastic potential energy is paramount, defined by the equation:
PE = (1/2)kx²
Here, ( k ) represents the spring constant—a measure of the spring’s stiffness—and ( x ) signifies the displacement from the spring’s equilibrium position. Conversely, kinetic energy is articulated as:
KE = (1/2)mv²
In this equation, ( m ) is the mass of the object attached to the spring, while ( v ) denotes its velocity. An astute understanding of these equations sets the foundation for all subsequent analyses.
2. The Principle of Conservation of Mechanical Energy
At the crux of solving spring energy problems lies the principle of conservation of mechanical energy. This principle posits that in the absence of external work or non-conservative forces (like friction), the total mechanical energy of an isolated system remains constant. Thus, as a spring compresses or elongates, energy transitions between kinetic and potential forms, but the total energy remains invariant:
Total Energy = KE + PE = constant
Recognizing this balance not only simplifies calculation but also underscores the interconnectedness of dynamic systems.
3. Identifying System Parameters
Upon understanding the fundamental energy transformations, the next step involves identifying the parameters of your particular spring system. Essential elements include the mass attached to the spring, the spring constant, initial displacement, and any external forces acting upon the system. Draw a diagram if necessary, illustrating the energy conversions at various positions of the spring. Visual representation often elucidates relationships that might be obfuscated in mere numerical form.
4. Setting Up the Energy Equation
Once parameters are understood, formulate the energy equation to describe how energy shifts from one form to another throughout the spring’s motion. If the spring is compressed or stretched, start by establishing the total mechanical energy at the maximum displacement point (where kinetic energy is zero and potential energy is at its peak). Conversely, at the equilibrium point, potential energy is zero while kinetic energy is maximized:
At maximum compression/stretch: PE = (1/2)kx₀²
At equilibrium: KE = (1/2)mv²
By juxtaposing these expressions, you can effortlessly glean insights into the relationships governing the motion of the spring-mass system.
5. Employing Calculus for Dynamic Scenarios
In more complex situations, where multiple oscillations or changing forces are at play, calculus becomes a formidable ally. By applying differential equations, you can derive expressions for position, velocity, and acceleration as functions of time. The relationship encapsulated within: ( F = -kx ) (Hooke’s Law), is a pivotal touchstone. Understanding how these variables interact over time empowers you to predict future states of the system and deduce maxima and minima efficiently.
6. Solving for Specific Quantities
To unravel any unknown parameters in your equations—be it velocity at a certain displacement or the work done by external forces—utilize algebraic manipulation alongside your established energy equations. By isolating variables, and leveraging the conservation principle, you can derive precise solutions systematically. As you solve, do not forget to re-evaluate units; dimensional consistency will reinforce the credibility of your findings.
7. Incorporating Damping and Real-World Applications
Efficiency in solving spring problems can be further enhanced by considering non-ideal real-world applications. Sudden damping forces often enter the fray in springs found in practical scenarios—like car shock absorbers. Integrate damping coefficients into your calculations to accurately simulate the mechanical dynamics at work. This not only fortifies the model against theoretical fracturing but also enriches your problem-solving repertoire.
8. Exploring Absolute Energy Levels
While balancing kinetic and potential energies provides a local view, considering absolute energy levels can enhance your understanding of a system’s behavior over time. In scenarios where external forces act, the system’s total energy shifts, and absoluteness can help predict eventual stasis or oscillation patterns. This global perspective fosters a deeper understanding of how kinetic and potential energies interact across the entire motion, stimulating even greater curiosity about the resultant dynamics.
9. Continuous Learning and Curiosity
Every spring system presents a unique challenge and an opportunity for intellectual growth. Engage deeply with each problem, allow curiosity to lead your exploration, and cultivate a fervor for uncovering the nuances of mechanical energy conservation. By approaching problems with both creativity and analytical prowess, each solution unveiled adds to your comprehensive understanding of the natural world’s remarkable interplay of forces.
In conclusion, approaching spring conservation of energy problems requires a solid grasp of basic principles, a systematic strategy for solving equations, and a willingness to adapt to the complexities of real-world applications. By employing these expert tips, one navigates through the labyrinth of energy with enlightenment and curiosity, emerging equipped to conquer any spring-related challenge with confidence.