Understanding the relationship between energy and mechanical systems is pivotal for anyone studying physics or engineering. One fundamental aspect of this relationship is the spring constant, denoted as ( k ), which describes the rigidity of a spring. In this practical guide, we will explore how to derive the spring constant using the principle of conservation of energy. This approach not only elucidates the mathematical framework behind springs but also underscores the intricate balance between potential energy and kinetic energy.
To begin our exploration, we must first familiarize ourselves with the Law of Conservation of Energy, which posits that the total energy in a closed system remains constant over time. This principle can be applied to elastic systems, where potential energy is stored when a spring is compressed or elongated. The stored energy can later be converted into kinetic energy as the spring returns to its equilibrium position.
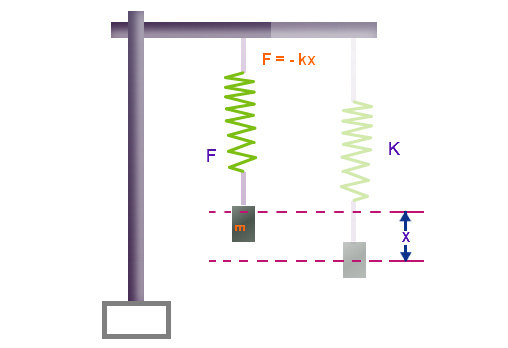
Firstly, let’s define the potential energy stored in a spring. The potential energy (( PE )) of a compressed or stretched spring can be expressed with the formula:
( PE = frac{1}{2} k x^2 )
where ( k ) is the spring constant (measured in Newtons per meter, N/m) and ( x ) is the displacement from the equilibrium position (in meters). This formula articulates that the potential energy is proportional to the displacement squared, emphasizing that a greater stretch or compression results in an exponential increase in potential energy.
Next, we need to consider the kinetic energy (( KE )) of the spring system. When the spring is released from its compressed or stretched state, the potential energy transforms into kinetic energy. The kinetic energy of an object in motion can be represented mathematically as:
( KE = frac{1}{2} mv^2 )
Here, ( m ) denotes the mass of the object attached to the spring, and ( v ) is its velocity just before it reaches the equilibrium position of the spring. At this juncture, all potential energy has converted into kinetic energy.
To ascertain the spring constant, we can apply the principle of conservation of energy. By setting the potential energy equal to the kinetic energy at the point of maximum displacement, we yield:
( frac{1}{2} k x^2 = frac{1}{2} mv^2 )
This relationship implies that at the equilibrium position, the mechanical energy of the system remains conserved. Upon simplifying the equation and eliminating the common factors, we arrive at:
( k x^2 = mv^2 )
From this expression, extracting the spring constant ( k ) is straightforward:
( k = frac{mv^2}{x^2} )
This formula provides a clear method for calculating ( k ) if one can measure the mass of the attached body, its velocity when passing through the equilibrium position, and the extent of compression or extension of the spring. To implement this in a practical experiment, several steps should be followed carefully.
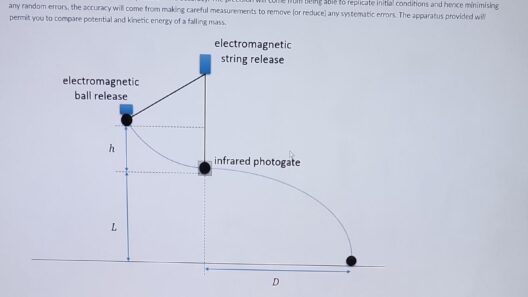
First, set up an apparatus that includes a spring, a mass, and a means to accurately measure displacement. It is crucial that the spring’s unstretched/unsquished position be clearly identified; this will serve as your reference point. Next, apply varying amounts of force to compress or stretch the spring, ensuring to record the corresponding displacement accurately. For each displacement value ( x ), you will need to measure the mass ( m ) and its velocity ( v ) as it passes through the equilibrium position.
To determine the velocity of the mass, you might consider utilizing a motion sensor or a high-speed camera. These tools enable precise measurements, capturing the velocity at the key moment when the kinetic energy is at its peak.
After gathering data for several trials, calculate the spring constant for each measurement using the derived formula ( k = frac{mv^2}{x^2} ). It is advisable to analyze multiple trials to ensure the accuracy of your data, averaging the results to arrive at a reliable spring constant. The more trials conducted, the more statistically significant your results will be.
While solving for the spring constant using conservation of energy provides precise results, it is also a gateway into a deeper understanding of energy transformations. Recognizing how energy shifts between forms when springs are engaged enriches the learning experience. Furthermore, this method exemplifies broader physics principles applicable in various domains such as engineering, architecture, and product design, where understanding material properties is critical.
In conclusion, the conservation of energy principle serves as a powerful tool to solve for the spring constant. By comprehensively grasping the interplay between potential and kinetic energy in a spring system, one can not only unravel the mechanics at play but also foster an appreciation for the elegance of physics. Science is not just about numbers and formulas; it invites us to appreciate the natural world’s intertwined connections. The quest for knowledge is continuous, much like the oscillations of a spirited spring returning to its resting state, full of potential energy ready to be released.