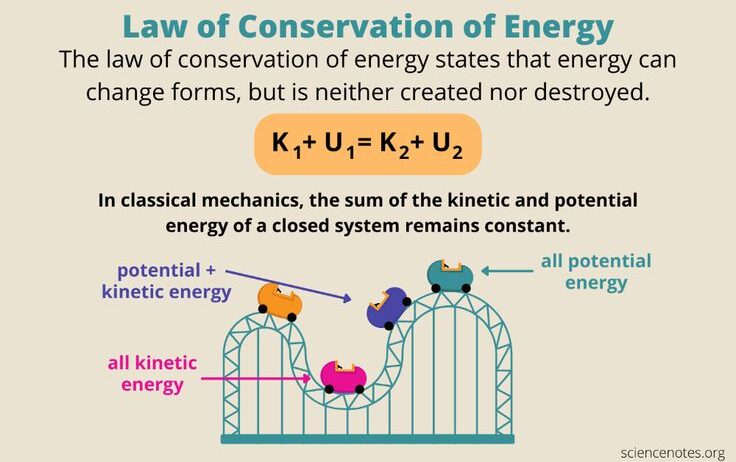
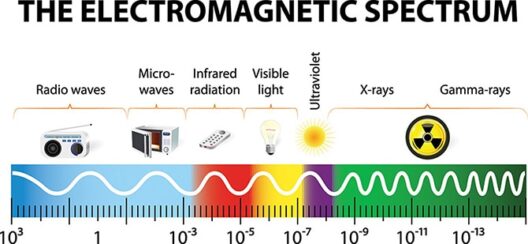
Understanding the Law of Conservation of Energy is pivotal in grasping the complexities of physics, environmental science, and various engineering disciplines. This foundational principle asserts that energy within a closed system remains constant; it can neither be created nor destroyed, merely transformed from one form to another. But how do we visually and mathematically demonstrate this profound concept? Let’s delve into this engaging journey of exploration, illustrated through both visual and numerical representations, and consider a playful question: What would happen in a world where energy could be created or annihilated at will?
To begin our examination, let’s clarify the essence of energy forms. Energy manifests in various forms, such as kinetic (energy of motion), potential (stored energy), thermal (heat), mechanical, electrical, chemical, and nuclear energy. The transformation between these types plays a critical role in numerous processes in the natural world and in human-engineered systems. For example, when a rollercoaster climbs to its peak, it accumulates gravitational potential energy that is converted into kinetic energy as it descends.
Visual proof of energy conservation can often be illustrated through a pendulum. As the pendulum swings, it transitions between kinetic and potential energy. At the highest points of its arc, the pendulum possesses maximum potential energy and minimal kinetic energy. Conversely, at its lowest point, it has maximum kinetic energy and minimal potential energy. If one were to neglect air resistance and friction, the sum of potential and kinetic energy throughout the swing remains constant, exemplifying the Conservation of Energy in a visually captivating manner.
Further enhancing this concept, one can employ innovative methods such as energy bar charts. Imagine constructing a bar graph that represents the different forms of energy in a given system. Take, for instance, a simple rollercoaster ride. As the coaster ascends, the height increases, which means that the potential energy bar rises proportionally. When it descends, the height decreases, yet the kinetic energy bar surges. Through these visual representations, it becomes evidently clear that while the forms of energy fluctuate, their total sum remains unchanged, thus enforcing the conservation principle.
Now, how do we mathematically substantiate the Law of Conservation of Energy? The principles hinge around just a few crucial equations. In the gravitational context, the potential energy (PE) can be defined as:
PE = mgh
Here, (m) represents mass, (g) is the acceleration due to gravity, and (h) is the height above a reference point. As potential energy transforms into kinetic energy (KE), which is given by:
KE = 0.5mv²
Where (v) signifies velocity. When a system operates without external influence, the total energy (TE) of the system can be encapsulated by:
TE = PE + KE
For every successful energy transition—from potential to kinetic and vice versa—total energy is sustained, reinforcing the conservation assertion. When these equations are graphed against time, one witnesses a sinusoidal wave behavior that visually reflects how energy oscillates yet remains conserved. It presents a rhythmic dance of transformation, one that illustrates the intrinsic balance of energy within our universe.
The implications of the conservation of energy extend far beyond mere physics; they stretch into real-world applications, including renewable energy technologies and sustainable practices. For instance, wind turbines convert the kinetic energy of air into mechanical energy, subsequently transformed into electrical energy, embodying this principle in action. Rendered harnessing energy from renewable sources is an essential step towards mitigating climate change, confronting the pressing challenge of shifting our dependence from fossil fuels to sustainable alternatives.
Now, let’s add a layer of complexity to our contemplation: Imagine a hypothetical scenario where there are fluctuations in energy that lead to its creation or destruction. What might the ramifications be? Perhaps limitless energy could usher in unprecedented advancements; however, it might also result in severe consequences for ecological balances. The exploration of energy conservation prompts inquiries that challenge our understanding of the universe’s laws while fostering inquisitiveness towards sustainable energy solutions.
To foster a deeper comprehension of the Law of Conservation of Energy, consider conducting experiments. One such engaging experiment involves a simple cart rolling down an inclined plane. Measure the cart’s heights at various intervals, calculating its potential and kinetic energy at each point using the corresponding formulas. Another engaging activity could involve observing the energy transfers in a bouncing ball. Each bounce can be quantified as it moves from potential energy at the apex to kinetic energy at the ground level. These hands-on activities not only solidify theoretical understanding but also foster a sense of curiosity and further exploration into energy systems.
In conclusion, showcasing the Law of Conservation of Energy through visual and mathematical proofs intertwines educational engagement with fundamental scientific principles. Through illustrative pendulum motions, energy bar charts, and rigorous computations, this essential law is not merely an abstract idea but a tangible and observable phenomenon. Importantly, understanding this principle invites us to reflect on our energy consumption and its broader implications on our planet. Embracing the responsibility of energy stewardship can amplify our efforts towards sustainable futures, conserving not just energy but nurturing the delicate balance of our environment.