The principle of conservation of energy is a profound concept in physics that states that energy cannot be created or destroyed; rather, it can only be transformed from one form to another. This principle serves as a fundamental crux for many applications within the realm of mechanics, particularly in determining the velocity of objects. Understanding how to leverage this principle can deepen one’s appreciation of both motion and energy dynamics. This guide will elucidate the steps to use the conservation of energy to find the velocity of an object in motion, along with illustrating critical concepts that underpin this fascinating interplay.
To comprehend the relationship between energy and velocity, one must first delineate the two pivotal forms of mechanical energy: potential energy (PE) and kinetic energy (KE). Potential energy is the stored energy due to the object’s position or configuration, while kinetic energy is the energy of an object in motion. Mathematically, these energies are expressed as:
Potential Energy (PE) = mgh
Kinetic Energy (KE) = ½ mv²
Where:
- m = mass of the object
- g = acceleration due to gravity (approximately 9.81 m/s² on Earth)
- h = height above a reference point
- v = velocity of the object
Now, contextually integrating these forms of energy with the conservation of energy principle, one can articulate that the total mechanical energy in a closed system remains constant, barring external work done on the system. This can be expressed as:
Total Mechanical Energy (TME) = PE + KE
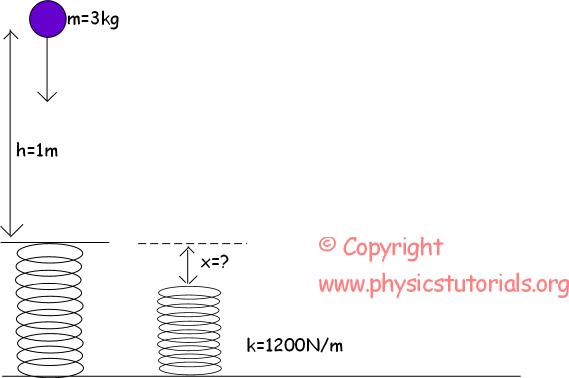
To delve into how to derive velocity using this principle, let us explore a common scenario: an object released from a certain height, free-falling under the influence of gravity. Initially, the object possesses gravitational potential energy, and as it descends, this potential energy is converted into kinetic energy.
Initially, at the height (h), the object’s energy can be characterized as:
Initial Total Energy (TME_initial) = PE + KE = mgh + 0 = mgh
Upon reaching a lower height (h’), the energy state changes. Here, we denote the height at this point as h’ (where h’ < h). The total mechanical energy now becomes:
Final Total Energy (TME_final) = PE + KE = mgh’ + ½ mv²
According to the conservation of energy:
TME_initial = TME_final
Thus, we can represent this as:
mgh = mgh’ + ½ mv²
On simplification, this equation presents a pathway to isolate the velocity:
mgh – mgh’ = ½ mv²
By factoring out m, we have:
gh – gh’ = ½ v²
Further redefining the variables gives:
g(h – h’) = ½ v²
Rearranging the terms, we find:
v² = 2g(h – h’)
Consequently, the velocity (v) of the object just before impact can be determined using:
v = √(2g(h – h’))
This foundational approach can be employed across various contexts where energy conservation persists, whether dealing with pendulums, roller coasters, or any system where elevation changes play a vital role. Key applications of these principles emphasize the importance of energy transformations in practical scenarios.
In addition to practical applications, it is paramount to understand how other forces may interject. In cases involving friction or air resistance, the energy accounted for will differ as some energy dissipates in the form of thermal energy due to these non-conservative forces. Therefore, a real-world framework often necessitates adaptation of the original formula to account for these factors.
For instance, when addressing friction, the work done by friction (f_d) diminishes total mechanical energy. Thus, the equation integrates this loss as:
mgh – f_d = ½ mv²
Understanding how to analyze various energy transformations enables one to gain a comprehensive perspective on the workings of motion. Observing the conservation of energy in multiple setups nurtures curiosity, compelling individuals to investigate deeper into the mechanics of their environment.
Utilizing these principles reveals insights not only about motion but also about the interconnectedness of different energy forms. Whether it is energy sourced from gravitational potential, elastic potential, or even chemical energy converted into kinetic movements, recognizing these conversions detours an exploration of a vast and enthralling subject. From bio-mechanics to astrophysics, the manifestations of these energy principles permeate far and wide. Engaging with these concepts might invoke one’s environmental consciousness, as understanding energy conservation can foster responsible energy usage, ultimately contributing to sustainability.
To conclude, mastering the principles of conservation of energy not only equips one with the ability to calculate velocity but also enhances one’s understanding of the natural world. This shift in perspective underscores the paramount significance of energy transformations in the intricate tapestry of motion. As we strive to comprehend and appreciate these foundational laws, we move closer to harnessing their potential for both intellectual and environmental realms.