The phenomenon of mechanical energy conservation is a fundamental principle in the realm of physics, particularly within the fields of classical mechanics and dynamic systems. It posits that in an isolated system free from external forces, the total mechanical energy—comprising kinetic and potential energy—remains constant over time. However, the question arises: Is the conservation of mechanical energy always valid? The answer to this inquiry is nuanced and requires a comprehensive examination of several pivotal concepts.
To grasp the validity of mechanical energy conservation, one must first understand the core definitions and classifications of energy. Mechanical energy is predominantly categorized into kinetic energy, which is the energy of motion, and potential energy, which is energy stored in an object’s position or configuration. The mechanical energy (E_m) of an object can be expressed mathematically as:
Em = K + U
where (K) denotes kinetic energy and (U) designates potential energy.
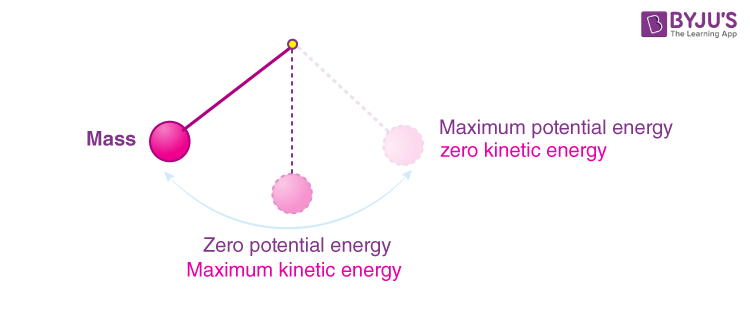
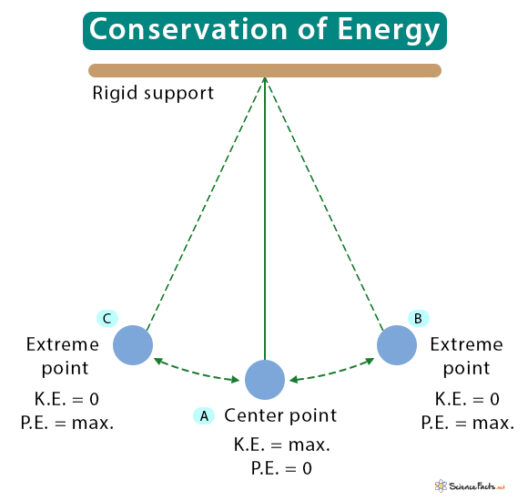
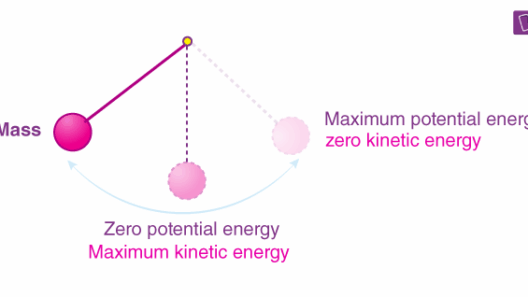
In an ideal and closed system, such as a frictionless pendulum swinging in a vacuum, the law of conservation of mechanical energy holds seamlessly; the energy transforms between kinetic and potential forms without any losses. For instance, at the highest point of its swing, potential energy is maximized while kinetic energy approaches zero. Conversely, at the lowest point, kinetic energy achieves its zenith while potential energy diminishes, illustrating a flawless energy interchange.
Nevertheless, a myriad of real-world scenarios disrupts this idealized perspective. The introduction of external forces, such as friction, air resistance, or drag, fundamentally alters the mechanical energy balance. In such cases, mechanical energy is dissipated in the form of heat, sound, or deformation, leading to a violation of energy conservation principles.
For example, consider a block sliding down an inclined plane. While it may appear that mechanical energy should be conserved, friction between the block and the surface converts a portion of the block’s mechanical energy into thermal energy, ultimately reducing the total mechanical energy of the system. The frictional force generates heat, impeding the block’s total kinetic energy. Consequently, understanding the absence of energy conservation requires examining work done by non-conservative forces.
Non-conservative forces are a critical element in the constellation of energy dynamics. These forces do not store energy within the system; instead, they typically convert mechanical energy into other forms. Friction is the archetype of non-conservative forces, but gravitational forces can also exhibit non-conservative behavior in certain contexts, such as during inelastic collisions. In these instances, energy may be dispersed in a manner not recoverable by the system, leading to permanent changes in mechanical energy.
The realm of energy conservation also extends into rotational dynamics, whereby the concepts of angular momentum and torque come into play. Rotating bodies, such as a spinning disk, showcase their own set of potential and kinetic energies. However, the introduction of torque—particularly non-conservative torque—can similarly lead to energy dissipation. If a torque acts on the system, it alters the rotational mechanical energy, again violating the conservation principle.
Furthermore, the conservation of mechanical energy is contingent upon the absence of external work being done on the system. If external forces do work—such as pushing a car up a hill—then the mechanical energy of the system can indeed change. Understanding the influence of external work is crucial in scenarios involving energy conservation analyses in engineering and technology.
A pertinent example can be found in roller coasters, where the design and operational mechanics are built around the conservation of mechanical energy. Two key forces—gravity and friction—play complementary roles. The coaster climbs to a height, accumulating potential energy, which is then transformed into kinetic energy as it descends. However, the influence of frictional forces at play means that not all the potential energy converts into kinetic energy, necessitating design adjustments to ensure sufficient speed at subsequent ascents or inversions.
Moreover, conservation principles can become convoluted in systems exhibiting complex interactions, such as coupled oscillators. In such systems, energy can be transferred between oscillating bodies, leading to the propagation of wave-like or harmonic functions. While total energy remains conserved, the mechanical energy of individual components may fluctuate in a manner that complicates straightforward assessments of mechanical energy conservation.
Interestingly, there are modern advancements in technology and innovative engineering practices that question established theories of energy conservation. Quantum mechanics introduces a distinct paradigm of energy interaction, wherein the discrete nature of energy quantization may yield unconventional behaviors that defy classical interpretations. This suggests a radical inquiry into the applicability of classical mechanical principles at atomic and subatomic levels, where the definitions of energy could evolve substantially.
In summary, while conservation of mechanical energy holds true under ideal circumstances devoid of external influences and energy losses, it becomes increasingly complex in real-world applications. Friction, non-conservative forces, external work, and specific system dynamics can undermine the simplicity of energy conservation theories. As the boundaries of physics and engineering continue to expand and evolve, a sophisticated understanding of mechanical energy conservation is paramount for both theoretical exploration and practical applications. It is an ever-relevant discourse, particularly given the pressing global need for sustainable energy solutions and efficiency in technological design.