In the realm of fluid dynamics, one may encounter a principle named after the Swiss mathematician Daniel Bernoulli, which elucidates the relationship between the velocity of a fluid and its pressure. This principle, articulated in the 18th century, has gained prominence not solely for its mathematical intrigue but also for its implications in various scientific and engineering applications. However, the question looms: does Bernoulli’s principle serve as a proof of energy conservation?
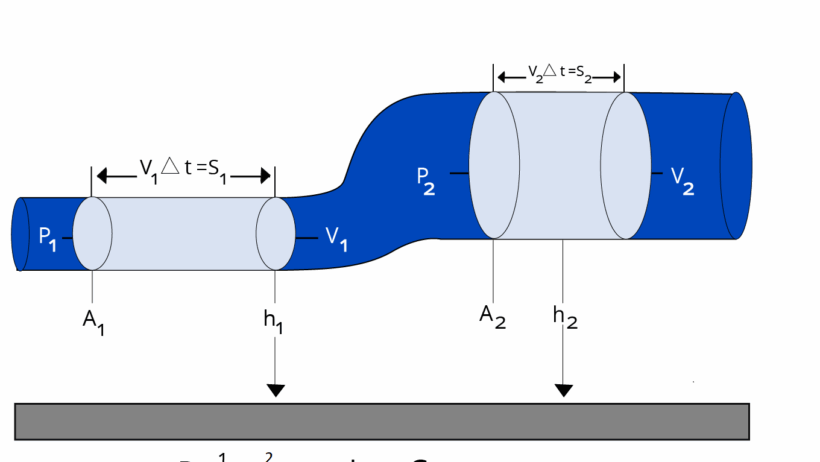
To unravel this inquiry, it is essential first to comprehend what Bernoulli’s principle posits. Simply stated, Bernoulli’s principle asserts that for an incompressible, frictionless fluid, the total mechanical energy along a streamline is constant. This total mechanical energy comprises three principal components: the kinetic energy due to the fluid’s velocity, the potential energy attributable to its elevation, and the pressure energy exerted by the fluid. In formulaic terms, it can be expressed as:
P + ½ρv² + ρgh = constant
In this equation, P represents the pressure energy, ρ signifies the fluid density, v is the fluid velocity, g is the acceleration due to gravity, and h signifies the elevation above a reference point. The invocation of this equation illustrates that a decrease in one form of energy must lead to a correlation in another: if the velocity of the fluid increases, then the pressure must decrease, and vice versa, thereby maintaining a consistent total energy value within the fluid stream.
When discussing the conservation of energy, it is pivotal to delineate between various forms of energy. The law of conservation of energy asserts that energy cannot be created or destroyed; it can only transform from one form to another. Bernoulli’s principle encapsulates this law within the context of fluid motion. By demonstrating that the total mechanical energy in a streamline remains constant, Bernoulli’s principle reinforces the conservation of mechanical energy specifically in fluid systems.
Yet, the implications of Bernoulli’s principle extend beyond mere mechanical energy. It nudges us to consider hydraulic systems and aerodynamics, environments in which energy conservation plays a paramount role. For instance, in aircraft wings, the shape and angle create differing airspeed above and below the wing. Thanks to Bernoulli’s principle, we can appreciate how faster air above the wing results in lower pressure compared to slower air underneath, thereby generating lift. This intricate dance of forces and energies underscores a tangible manifestation of energy conservation in action.
However, some may contend that Bernoulli’s principle does not apply universally. Isolated systems may exhibit anomalies where energy dissipation occurs, primarily due to friction and turbulence, which disrupt the idealized conditions Bernoulli proposed. In such cases, the non-conservative forces at play can lead to energy loss in the form of heat, sound, or other unwanted emissions. These deviations remind us that while Bernoulli’s principle holds for ideal circumstances, real-world complexities must be acknowledged. Energy conversion mechanisms—including thermal dissipation—challenge the notion of strict energy conservation within dynamic and turbulent scenarios.
A noteworthy perspective arises when considering Bernoulli’s contribution to the broader discourse on energy conservation. Rather than viewing it solely as a mathematical construct, we may pivot our perspective to embrace the elegant interconnections embedded within fluid dynamics. This principle urges us to recognize the myriad interactions that occur in the natural world, often overlooked in a landscape rife with focus on singular energy forms. As we contemplate water flow, air traffic, and the symbiosis of ecosystems, it becomes evident that the interconnectedness Bernoulli illustrated holds profound implications for our understanding of energy in nature.
Furthermore, invoking Bernoulli’s principle in discussions about environmental sustainability can be particularly enlightening. For example, examining how efficient fluid dynamics can enhance energy systems reveals an intriguing nexus between physical laws and ecological responsibility. Innovations that harness wind energy, water vortex turbines, or optimized combustion engines can all trace their efficacy back to Bernoulli’s insights. As societies strive for cleaner energy solutions, the foundational knowledge bestowed upon us by this principle acquires renewed relevance, showcasing its role as a catalyst for technological advancement.
In summary, while Bernoulli’s principle does not serve as irrefutable proof of energy conservation, it encapsulates the essence of mechanistic energy preservation within fluid systems. It invites us to ponder the intricacies of energy transformations and propels us toward a nuanced understanding of its applications in both theoretical and practical realms. The interplay of velocity, pressure, and elevation as dictated by this principle illustrates the wonders of physics at work, challenging us to appreciate the subtleties inherent in energy’s many forms. As we navigate our way into an increasingly complex future, embracing Bernoulli’s insights may aid in fostering sustainable practices and innovations that honor the delicate balance of energy conservation in our everyday lives.