In the realm of physics, collisions are a fundamental concept that reveals much about the laws governing energy and momentum. Among the various types of collisions, oblique impact collisions are particularly fascinating. These occur when two objects collide at an angle, resulting in a complex interplay of forces and energy transformation. But the pivotal question arises: is energy conserved in these collisions? To explore this, one must delve into the intricacies of kinetic energy, momentum, and the nature of collisions themselves.
Firstly, it is imperative to differentiate between elastic and inelastic collisions. In an elastic collision, both kinetic energy and momentum are conserved. This means that after the collision, the total kinetic energy of the system remains the same as it was before the impact. On the other hand, in inelastic collisions, while momentum is conserved, kinetic energy is not. Some of the energy is transformed into other forms, such as heat, sound, or even deformation of the objects involved. Understanding this dichotomy is essential when investigating energy conservation in oblique impact collisions.
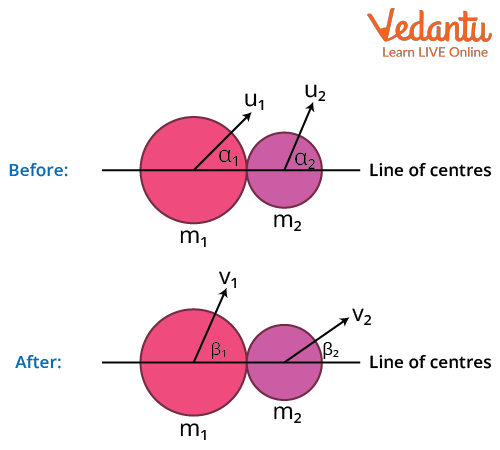
When two bodies collide obliquely, the angles at which they meet influence both the conservation of momentum and kinetic energy. The analysis begins with the conservation of linear momentum, a principle asserting that the total momentum of a closed system before the collision equals the total momentum after. This holds true regardless of the nature of the collision. In the case of oblique impacts, momentum must be resolved into its vector components—usually along the x and y axes. This resolution allows for a more straightforward application of the conservation laws, as the problem can be broken into two-dimensional analyses.
To illustrate this principle, consider two billiard balls colliding on a table. If one ball (Ball A) strikes another (Ball B) at an angle, the direction and magnitude of their velocities will change post-collision. By calculating the momenta in both the x and y directions before and after the collision, it becomes evident that while momentum remains conserved, the kinetic energy may not, depending on whether the collision is elastic or inelastic.
In an oblique collision, we can visualize the collision as comprising two distinct processes: the approach and the subsequent separation of the objects. During approach, kinetic energy is stored as potential energy due to the deformation that may occur, especially in inelastic collisions. Herein lies a captivating aspect of oblique collisions—the transformation of energy is not always straightforward, and energy dissipation can occur in varied forms. This complexity piques interest because it leads us to consider not merely if energy is conserved, but how energy is reallocated within the system.
The transition from kinetic to potential energy highlights the non-linear relationship between energy forms during such interactions. This phenomenon intrigues physicists and engineers alike, especially when applied to real-world scenarios, such as automobile collisions or even molecular interactions in material sciences. In such cases, understanding energy conservation becomes pivotal for safety and efficiency. For instance, crumple zones in cars are designed to absorb energy—transforming it rather than conserving the initial kinetic energy, safeguarding passengers by reducing the acceleration forces they experience during a collision.
Nonetheless, changes in energy during oblique impact collisions can also provide valuable insights into material properties and structural integrity. When conducting experiments or simulations, researchers often find that the angle of impact, relative masses of the colliding bodies, and their material compositions significantly influence outcomes. Such variations underscore a shift in perspective: what may appear as a mere loss of energy is, in fact, an intricate dialogue between physical properties, energy allocation, and the inherent characteristics of colliding materials.
A noteworthy point of discussion involves energy dissipation. Unlike kinetic energy, which is often easily quantified, the energy transformed into sound, heat, or structural deformation poses challenges for accurate calculation. This uncertainty urges a reconsideration of how energy conservation is approached theoretically versus practically applied in various fields, including engineering and sports science. The implications extend far beyond simple calculations, pushing the boundaries of material design, safety equipment development, and even athletic performance optimization.
In conclusion, while momentum is undeniably conserved in oblique impact collisions, the fate of kinetic energy begs deeper contemplation. Whether it is conserved or transformed depends intricately on the nature of the collision and the characteristics of the objects involved. This nuanced understanding emphasizes that energy conservation is not merely a binary state; rather, it encapsulates a complex interplay of physics principles, material behaviors, and innovative applications.
This discussion invites curiosity and sparks intrigue among those who delve into the science of collisions—transforming a seemingly simple question into an exploration of fundamental physical laws and their real-world implications. Navigating the intricate dynamics of oblique impact collisions allows one not only to grasp essential physical principles but also to appreciate the rich tapestry of interactions that govern the natural world.