When contemplating the realm of oscillatory motion, especially in contexts relating to physics, one might ponder whether energy remains preserved in systems characterized by damping. The phenomenon of damped oscillation introduces a fascinating interplay between energy and resistance, igniting curiosity about the foundational principles governing these behaviors.
Damped oscillators are systems that experience a gradual loss of energy over time, primarily due to dissipative forces like friction or air resistance. This contrasts sharply with their undamped counterparts, where energy conservation is a hallmark of their oscillatory nature. The intricacies of energy transfer in damped systems challenge traditional assumptions regarding the perpetuation of energy in mechanical systems. So, does energy have the same staying power in damped oscillators as it does in idealized models?
To effectively address this question, one must first understand the fundamental principles underpinning harmonic oscillators. An ideal harmonic oscillator is characterized by a restoring force that is directly proportional to its displacement from equilibrium, resulting in periodic motion. In such systems, energy oscillates between potential and kinetic forms, and the total mechanical energy remains constant as long as no external forces act upon it.
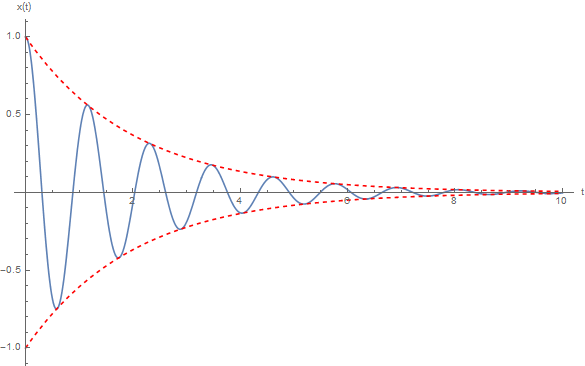
However, the introduction of damping disrupts this equilibrium. Damping forces, which act in opposition to the direction of motion, create a scenario where energy is not merely redistributed but gradually dissipated as thermal energy. This dissipation can be attributed to various factors, including internal friction within materials or the resistance offered by the medium through which the oscillator moves. A common example of damping can be found in a pendulum swinging through air; over time, it loses amplitude until it eventually comes to rest.
This leads us to the crux of the inquiry: Is energy genuinely conserved in damped oscillators? The answer requires a multifaceted exploration. In a strict sense, the total mechanical energy of a damped oscillator decreases over time, indicating that energy is not conserved within the system itself. As the oscillation proceeds, energy is transformed into other forms, primarily thermal energy, which disperses into the environment. Thus, while the energy is conserved in the broader context of the universe—where it cannot be created or destroyed—it is not conserved in the energy balance of the damped system in isolation.
To elaborate, consider a damped harmonic oscillator represented mathematically by a differential equation that incorporates a damping term. Analyzing the motion reveals an exponential decay of the amplitude over time. The energy of the system dwindles as energy is dissipated. In essence, though the system participates in energy transfer, it does not maintain energy in its mechanical form. Over time, the amplitude of the oscillations diminishes, reflecting this loss of energy.
Intriguingly, damped oscillators not only illustrate the loss of energy but also bear implications for various applications in engineering and technology. They serve as critical components in the design of structures and materials, especially in seismology and vibration control. Understanding the principles of damping allows architects and engineers to create buildings that withstand earthquakes through tuned mass dampers, which absorb and dissipate vibrational energy during seismic events. This application highlights the practical significance of analyzing energy dissipation.
Moreover, the phenomenon of damping extends beyond mechanical systems. In the realm of electromagnetism, for instance, damped oscillations appear in circuits containing inductance and resistance. Here, the energy loss manifests as a decay in the oscillatory current over time, analogous to mechanical damped systems. These parallels illustrate that the loss of energy in oscillatory systems is a universal principle, transcending disciplines while maintaining a common thread—whether through mechanical motion or electrical currents, damping illustrates a critical mechanism of energy transformation.
As one dives deeper into the concept of damping, an intriguing concept arises: the notion of “critical damping.” This state represents the exact threshold between oscillation and non-oscillation, leading to the swift return of a system to its equilibrium position without overshooting. Understanding critical damping not only reinforces the importance of energy dissipation but also prompts inquiries into optimizing systems for efficiency and stability.
Nonetheless, in the natural world, many systems exhibit damped behavior that is not as easily optimized. For example, biological systems, including the biomechanics of human motion, often encounter damping due to muscle friction, air resistance, and other dissipative forces. Recognizing these damped processes can inform better design in robotics and biomechanics, where energy efficiency is of paramount importance.
In conclusion, the inquiry into whether energy is conserved in damped oscillators reveals more than a mere answer—it unveils a complex tapestry of energy transformation and dissipation that resonates through both theoretical physics and practical applications. While it is evident that damped oscillators experience a loss of mechanical energy, this insight paves the way for innovations across a spectrum of disciplines. Ultimately, an understanding of damping may inspire curiosity, urging individuals to reconsider how energy flows and transforms in the myriad systems of our world, fostering an appreciation for the delicate balance between energy conservation and dissipation that underpins the natural order.