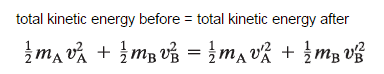When considering motion, one often imagines objects traversing linear paths—the straightforward journey of a ball rolling down a hill or a car speeding down a highway. However, the world of physics extends far beyond these linear trajectories. As we delve into the intricacies of rotational motion, a new dimension of kinetic energy emerges, inviting us to explore whether it too observes the law of conservation. This discussion will illuminate the delightful complexities of rotational kinetic energy and investigate its conservation principles.
To grasp the concept of rotational motion, think of a spinning top. As it twirls, it maintains a delicate balance, gracefully transforming energy from one form to another. Rotational kinetic energy (RKE) is the energy possessed by an object due to its rotation around an axis. Mathematically, it is expressed as ( KE_{rot} = frac{1}{2} I omega^2 ), where ( I ) stands for the moment of inertia and ( omega ) represents the angular velocity. Now, consider the moment of inertia as the rotational counterpart of mass; it measures how difficult it is to change the rotational state of an object. Just as mass influences linear motion, the distribution of mass about an axis of rotation plays a critical role in RKE.
Conservation of energy is a cornerstone principle in physics, asserting that energy cannot be created or destroyed, only transformed from one form to another. This concept holds true whether we are discussing linear or rotational motion. In an isolated system, where external torques are absent, the total mechanical energy remains constant. However, when analyzing diverse scenarios—such as elliptical orbits of planets or the majestic pirouettes of a figure skater—one must approach the topic of conservation with nuance.
Imagine a high-speed chase scene. As the car speeds up, it burns fuel, converting chemical energy into kinetic energy, both translational and rotational. The tires rotate, creating motion while experiencing friction—the resistance that often dissipates energy in the form of heat. Here, energy transitions are evident, but the precise pathways it traverses can be elusive. While it might seem that rotational kinetic energy can easily be lost through heat, one must not be misled; in the absence of friction, all initial kinetic energy can be conserved during purely rotational motions. This introduces the concept of energy dissipation and the subtle losses incurred during real-world applications.
Taking a closer look at conservation principles, consider a figure skater executing a spin. As she draws her arms inward, her moment of inertia decreases—resulting in an increase in her angular velocity due to the conservation of angular momentum. This counterintuitive phenomenon underscores a fundamental truth: while kinetic energy may not be conserved in isolation due to transformations, angular momentum remains steadfast. Their interplay highlights the remarkable choreography present in the physical universe.
Beyond mere physical exemplifications, the implications of rotational motion can be tied to broader themes of conservation and sustainability. In a world increasingly reliant on energy efficiency, understanding rotational dynamics provides vital insights, not just within realms of physics, but also in engineering applications driving renewable energy technologies. Wind turbines, for instance, harness rotational kinetic energy. As they rotate, they convert the kinetic energy of wind into electrical energy—a tantalizing symphony of energy transformation.
Consider the Earth, spinning relentlessly on its axis—a grand celestial body orchestrating its radial ballet through space. Its own rotation contributes to the conservation of energy on a planetary scale. As we observe our planet’s rotation and its resultant effects on climate and ecology, it becomes evident that the principles of rotational kinetic energy have profound implications. Understanding how energy circulates within natural systems can lead us toward sustainable practices that respect and protect our environment.
Yet, the question of conserved energy in rotational motion invites scrutiny. In rotating systems where friction and air resistance cannot be ignored, energy is indeed not conserved in the context of mechanical energy alone. The lost energy transforms into heat, resonating with the second law of thermodynamics, which highlights the natural progression towards disorder in isolated systems. This interplay between order and chaos shapes the dance of energy in our universe.
Thus, while rotational kinetic energy can be transferred, transformed, and dissipated, it can, under specific conditions, maintain a balance—a consideration crucial to both theoretical physics and practical applications. A thorough investigation reveals that in scenarios devoid of external forces or dissipative processes, rotational kinetic energy embodies the conservation ideal. However, real-world environments seldom permit such perfection, making the study of energy transformations an evolving discourse.
The realm of rotational motion is a captivating tapestry woven from intricate threads of physics, nature, and technology. Each spin, each revolution tells a story of energy in transit, showcasing the resilience of conservation principles whilst illustrating the inevitability of transformation. As we navigate through these layers of complexity, it becomes palpable that understanding kinetic energy—both linear and rotational—equips us with the necessary insights to engage with the challenges of sustainability, embracing a future where energy conservation reigns supreme.