Understanding the relationship between kinetic energy and the equation PV = nRT necessitates delving into the realms of thermodynamics, a branch of physics that governs the behavior of heat and energy transfer. This discussion serves to illuminate a fundamental question: Is kinetic energy conserved in systems described by this state equation? To answer this, we will explore the principles behind kinetic energy, delve into the ideal gas law encapsulated in PV = nRT, and evaluate how energy conservation principles apply across various thermodynamic processes.
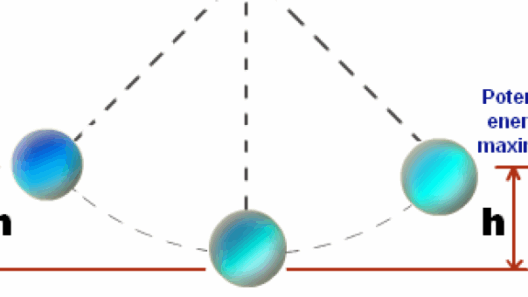
To begin, we must define kinetic energy. This form of energy is defined as the energy an object possesses due to its motion and can be quantified using the formula K.E. = ½mv², where m is mass, and v is velocity. Kinetic energy is inherently linked to the movement of molecules within a substance. As temperature increases, the speed of these molecules typically escalates, thus enhancing the kinetic energy of the system.
In contrast, the equation PV = nRT, known as the ideal gas law, describes the state of an ideal gas through the interrelationship of pressure (P), volume (V), the number of moles (n), temperature (T), and the universal gas constant (R). This relationship posits that any alteration in one of these variables necessitates a compensatory change in the others, provided the gas behaves ideally. The ideal gas law encapsulates thermodynamic properties critical for various applications and scientific explorations.
At first glance, one might not intrinsically connect kinetic energy with the ideal gas law. However, an exploration of each term reveals that the temperature (T) in the ideal gas law is directly proportional to the average kinetic energy of the gas molecules, as per the equation KE_avg = (3/2)kT, where k is the Boltzmann constant. This establishes a direct correlation: as the temperature of a gas increases, so does the average kinetic energy of its molecules.
In thermodynamics, energy conservation is pivotal. The first law of thermodynamics stipulates that energy cannot be created or destroyed, only transformed from one form to another. This law applies universally, encompassing all forms of energy, including kinetic. In an isolated system, the total energy remains constant. However, kinetic energy can undergo transformation during dynamic processes, such as expansion or compression in gases.
To consider the dynamics within a gas, we can analyze two scenarios: an adiabatic process and an isothermal process. In an adiabatic process, no heat is exchanged with the surroundings. Here, as a gas expands, it does so at the expense of its internal energy, which translates to a drop in temperature, hence reducing kinetic energy. Although the total energy is conserved, the kinetic energy transforms into potential or internal energy, illustrating that while kinetic energy can diminish in certain conditions, conservation principles remain intact.
Conversely, in an isothermal process, the temperature of the gas remains constant. Consequently, the average kinetic energy of the gas molecules is constant throughout the process. In this scenario, when a gas expands or contracts, heat is exchanged with the environment—energy flows into or out of the system—thereby maintaining constant kinetic energy despite changes in pressure and volume. This contrasting examination illustrates how kinetic energy behaves differently under various thermodynamic conditions while adhering to the overarching laws of energy conservation.
Another key consideration is the role of collisions in a gas. The kinetic theory of gases posits that gas pressure arises from the cumulative effect of countless molecular collisions against the walls of a container. Each collision involves a transfer of kinetic energy—a process governed by conservation laws. Despite individual molecules gaining or losing kinetic energy during interactions, the average kinetic energy remains consistent under stable conditions. This aspect underscores the importance of examining macroscopic quantities, such as temperature, which gives insight into the average kinetic energy level of a system as a whole.
The interplay between kinetic energy and the ideal gas law compels us to rethink conventional understandings of energy conservation. In exploring kinetic energy in different states and processes, we can discern that energy may transform forms but remains conserved overall. The phenomena observed in gaseous systems provide a fascinating lens through which to examine broader energy dynamics prevalent in nature.
Ultimately, the relationship between kinetic energy and the ideal gas law prompts us to reconsider energy conservation’s implications, fostering a rich discourse on how energy moves and transforms within our universe. Through a rigorous investigation of this interplay, we can broaden our perspectives on energy use and conservation in practical applications, from atmospheric science to engineering practices, cementing the importance of these principles in fostering a sustainable future.
In conclusion, while the query regarding the conservation of kinetic energy in relation to the equation PV = nRT leads to complex implications in thermodynamic processes, the essence remains clear: kinetic energy may fluctuate and transform under various conditions yet persists as a conserved entity within the ultimate framework of energy dynamics. Understanding these connections invites an exploration of energy conservation that is crucial to addressing contemporary environmental challenges.