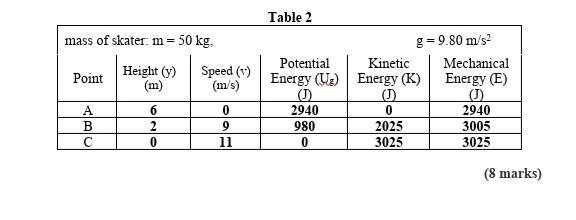
In the realm of classical mechanics, the principle of conservation of mechanical energy is a pivotal concept that provides profound insights into the dynamics of physical systems. Particularly compelling is the inclined plank setup, often utilized in laboratory demonstrations to illuminate the interplay between potential and kinetic energy. This analysis not only addresses a fundamental inquiry concerning the conservation of mechanical energy but also unveils the underlying principles that govern motion and energy transformations.
To set the stage, consider an object, such as a block, positioned at the apex of an inclined plane. At this juncture, the object possesses gravitational potential energy, calculated through the product of its mass, the acceleration due to gravity, and the height relative to the bottom of the incline. As the block begins its descent, gravitational potential energy is systematically converted into kinetic energy, which is defined as the energy an object possesses due to its motion. The kinetic energy of the block is quantified by the relationship K.E. = 0.5 * m * v², where m stands for mass and v indicates velocity.
As the block traverses down the inclined plank, one might intuitively presume that the total mechanical energy remains constant, adhering strictly to the law of conservation of energy. This principle stipulates that, in the absence of external forces, the total mechanical energy of a system—comprising both kinetic and potential energy—should indeed remain invariant. However, real-world observations frequently deviate from this idealized notion, prompting an exploration into the deeper reasons for energy dissipation.
Friction serves as a primary villain in this narrative. In any practical experimental setup, the inclined plane ceaselessly engages in interactions with the block, generating resistive forces that act counter to the direction of motion. The presence of friction introduces an energy sink, where a fraction of the mechanical energy is transformed into thermal energy. This dissipation manifests as heat, resulting in a scenario where the total mechanical energy is not conserved. Ultimately, the block would descend slower and possess less kinetic energy upon reaching the base of the incline than one would anticipate if friction had been negligible.
Moving beyond friction, one must also consider other factors that might influence mechanical energy conservation. Air resistance, albeit less significant than friction, can contribute to energy losses during motion. As the block accelerates, the surrounding air molecules produce drag, further diminishing the kinetic energy as a function of speed. Hence, the nuances of energy transformation in the presence of these dissipative forces reveal a more intricate picture—a dynamic interplay where energy does not simply vanish but transitions into other forms.
This invites additional considerations about the configuration of the inclined plane itself. The angle of inclination, surface texture, and material properties all correlate with the magnitude of frictional forces. A steeper incline may expedite the descent of the block, yet the increment in velocity can also exacerbate air resistance. Furthermore, examining different materials—as in wood, metal, or plastic—will showcase various coefficients of friction, with some facilitating smoother motion than others and influencing the energy conservation outcomes differently.
Another layer of complexity lies within the concept of elastic potential energy, particularly if the block interacts with springs or other elastic materials. Should the block collide with a spring at the bottom of the incline, the gravitational energy originally derived from the height of the incline may convert partially into elastic potential energy. This points to a scenario where the conservation of mechanical energy remains valid within the confines of the overall system, yet it is redistributed among various forms of energy rather than being visibly conserved as kinetic energy alone.
Extending the analysis further, one can integrate a more sophisticated view of mechanical energy conservation involving rotational dynamics. If the inclined plane rotates—say, about a horizontal axis—the interplay between translational and rotational kinetic energies adds an additional layer of complexity to the system. In this context, the total mechanical energy of the system must encompass not only the translational kinetic energy of the block but also the rotational kinetic energy attributed to the motion of the inclined plane itself.
As we delve deeper into this topic, it becomes evident that understanding the nuances of mechanical energy conservation in the inclined plank setup transcends mere calculations. It provokes inquiries into core principles of physics and the intrinsic properties of materials. From simple classroom experiments to sophisticated physics competitions, the principles governing energy conservation remain a fundamental exploration into the nature of our universe.
The fascination with mechanical energy conservation extends into practical applications, impacting engineering design, environmental sustainability, and even recreational activities such as roller coasters and amusement park rides. Each of these domains relies on the meticulous balancing of forces and energy transformations—capitalizing on the principles uncovered through the study of inclined planes. Ultimately, the determined pursuit of knowledge surrounding mechanical energy conservation not only illuminates the path of scientific inquiry but also reinforces the significance of energy efficiency in our everyday lives.