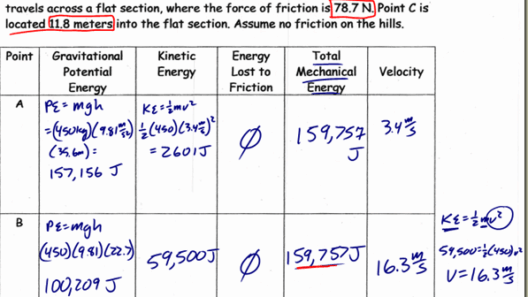
When pondering the enigmatic dance of energy within our universe, one often stumbles upon the pivotal concept of mechanical energy, which is the confluence of kinetic energy and potential energy. Imagine, if you will, a grand orchestration—the kinetic energy, like a sprightly dancer leaping across the stage, and potential energy, akin to a coiled spring poised to release its latent energy. Together, their sum is often heralded as an unassailable sentinel of conservation. But is it truly immutable? Let us embark on a journey to explore the intricacies surrounding this question.
To comprehend whether the sum of kinetic and potential energy is conserved, one must first delineate the definitions of these energies. Kinetic energy embodies the energy of motion; an object in movement possesses kinetic energy relative to an observer. It can be quantified using the formula ( KE = frac{1}{2}mv^2 ), where ( m ) represents mass and ( v ) represents velocity. Conversely, potential energy encapsulates the energy stored within an object due to its position, arrangement, or state. For instance, an object at a certain height possesses gravitational potential energy given by ( PE = mgh ), where ( g ) is the acceleration due to gravity and ( h ) is the height above a reference point.
The principle of conservation of mechanical energy postulates that in an isolated system—one devoid of external forces—the total energy remains constant. It is here that the sum of kinetic and potential energy holds its ground. Picture a pendulum; as it swings from its highest point, potential energy transforms into kinetic energy. At the apex, kinetic energy is at its nadir while potential energy is at its zenith. As the pendulum descends, potential energy diminishes in favor of an escalating kinetic energy, until the lowest point where kinetic energy reaches its maximum. It appears to be a seamless symphony, each note effortlessly transitioning to the next.
However, the allure of this scenario is deceptively simplistic. Real-world applications often introduce variables that can disrupt this harmony. Friction, air resistance, and other forms of dissipative forces act as antagonists in this narrative. For instance, consider a roller coaster navigating its thrilling ebbs and flows. As it negotiates curves and dips, not all potential energy is converted into kinetic energy due to the inescapable presence of friction and thermal energy losses. The roller coaster’s descent, rather than being a meticulous exchange of energies, devolves into a process where the total energy decreases, eroding the conservation principle within this particular context.
Some may argue that although total mechanical energy is not conserved in such systems, the law of total energy conservation remains steadfast. This principle posits that while mechanical energy may transform into other forms—such as thermal energy due to friction—the total energy of the system remains unchanged. Yet even this premise invites scrutiny. In practical scenarios, one can continuously feed energy into the system or extract energy from it, complicating the notion of a closed system.
Moreover, when delving deeper into more complex systems, such as those involving rotational motion or inelastic collisions, the conservation of mechanical energy further muddles. Inelastic collisions, unlike elastic ones, involve energy dissipation into other forms, such as heat, sound, or permanent deformation. It is in such environments that the pristine concept of energy conservation becomes a labyrinthine challenge, fraught with complications and nuances.
As we further explore the realms of quantum mechanics, the story of energy conservation becomes even more intriguing. In this domain, energy takes on characteristics that defy traditional notions. The principle of uncertainty introduces elements of probability and unpredictability, leading one to question the deterministic nature of energy conservation at microscopic scales. One might liken this to a game of cosmic hide and seek, where particles masquerade as both waves and particles, ephemeral yet influential in their interactions.
In the grand tapestry of conservation laws, it is essential to acknowledge that while the sum of kinetic and potential energy may serve as a reliable measure under ideal circumstances, one must remain vigilant and adaptable in the face of real-world phenomena. Energy interactions are as fluid as water coursing through a river—elastic and capricious, shifting extensively with changes in external forces. Thus, the sanctity of the conservation principle may not always be as unwavering as initially perceived.
As we engage with this multifaceted subject, consider this: sustainability and conservation are not merely about adherence to abstract principles; they are about recognizing and respecting the natural dynamics of energy in our environment. Each action we take reverberates through our interconnected ecosystems. When approaching energy use and conservation, it is paramount to integrate an understanding of the myriad interactions that take place—some transparent and others hidden within the complexities of nature.
In conclusion, the sum of kinetic and potential energy, while a valuable concept in ideal systems, must be approached with discernment when applied to the tangible world we inhabit. The vibrancy of life, the myriad forms it takes, and our capacity to manipulate energy all play a role in shaping our understanding of conservation. The interplay of energies is a vivid reminder that within the grand theater of the universe, every act of energy transformation carries echoes of both creation and loss, inviting us to tread lightly and thoughtfully in our pursuits.