Conservation of energy is a fundamental principle in physics that plays an essential role in understanding how objects interact with their environment. Imagine a scenario: you are holding a ball high above the ground and about to release it. Have you ever thought about what happens to the energy contained in that ball as it begins to fall? This playful question introduces the fascinating challenge of unraveling the concept of energy conservation in the context of a falling object.
At its core, the principle of conservation of energy states that energy cannot be created or destroyed, only transformed from one form to another. When you drop the ball, gravitational potential energy is gradually converted into kinetic energy as it accelerates toward the ground. In order to appreciate this transformation, let us delve deeper into the concepts of potential and kinetic energy.
Potential energy, specifically gravitational potential energy (GPE), is the energy that an object possesses due to its height above a reference point, typically the ground. The formula to calculate gravitational potential energy is given by:
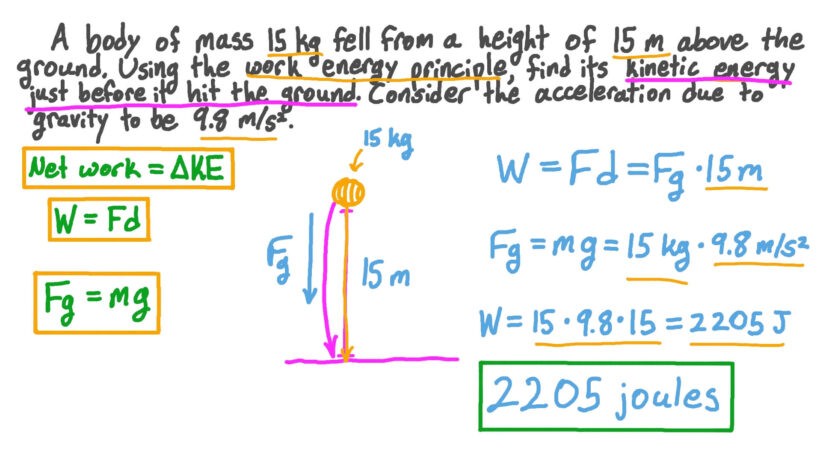
GPE = mgh
Where m represents the mass of the object (in kilograms), g is the acceleration due to gravity (approximately 9.81 m/s² on Earth), and h is the height (in meters) above the reference point. For instance, if our ball weighs 2 kilograms and is held 10 meters above the ground, we can calculate its gravitational potential energy as follows:
GPE = 2 kg * 9.81 m/s² * 10 m = 196.2 Joules
This indicates that the ball has 196.2 Joules of energy, waiting to be unleashed. When the ball is released, this potential energy is transformed into kinetic energy, which is the energy of motion. The formula for kinetic energy (KE) is expressed as:
KE = 0.5 mv²
Where v represents the velocity of the object just before impact. This transformation of energy is not merely theoretical; it encompasses all physical interactions when dealing with falling objects.
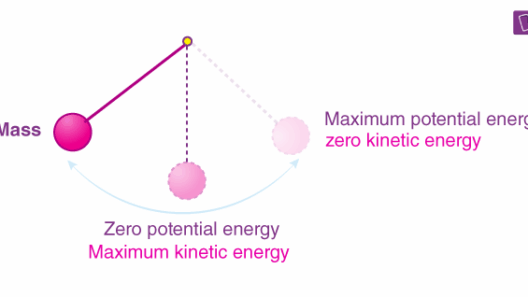
To understand this transformation clearly, consider the path of the falling ball. As the ball descends, its height decreases, thus its potential energy diminishes. Simultaneously, its velocity increases, resulting in an increase in kinetic energy. The total mechanical energy (TME) of the ball—comprising both potential and kinetic energy—remains constant throughout its drop, illustrating the conservation of energy principle:
TME = GPE + KE = constant
When the ball is at its highest point, all the energy is in the form of potential energy, and at the moment just before it strikes the ground, all the energy has been converted into kinetic energy. This understanding poses a potential challenge: can you visualize the moment just before the ball hits the ground? How fast is it moving, and how much kinetic energy does it possess?
To find out, consider the speed of the ball at the moment of impact. Assuming no air resistance, we can determine the final velocity of the ball upon reaching the ground using the following kinematic equation:
v² = u² + 2as
In this formula, u is the initial velocity (0 m/s when released), a is the acceleration due to gravity (9.81 m/s²), and s is the distance fallen (10 m). Plugging in the values:
v² = 0 + 2 * 9.81 * 10
v² = 196.2
v = √196.2 ≈ 14.0 m/s
This calculation reveals that at the point of impact, the ball is traveling at a speed of approximately 14 m/s. Integrating this value into the kinetic energy formula allows us to find the kinetic energy just before the ball strikes the ground:
KE = 0.5 * 2 kg * (14 m/s)² = 196 Joules
This aligns perfectly with our initial potential energy calculation, demonstrating the conservation of energy principle. The ball’s energy merely transitioned from one form to another—undoubtedly an eloquent ballet of physics in motion.
Now contemplate real-world implications. Understanding the conservation of energy is not just an academic exercise; it holds substantial significance in various domains, such as engineering, environmental science, and safety protocols. For example, engineers apply these concepts to design safer playgrounds with energy-absorbing materials. In environmental science, awareness of energy conservation fosters sustainable practices by minimizing waste and optimizing resource usage.
Moreover, consider the broader context of energy conservation in our daily lives. The principle encourages us to recycle, to reuse materials, and to embrace renewable energy sources. As stewards of our planet, those who grasp these concepts can inspire others to innovate and adopt strategies that promote energy efficiency.
In conclusion, the energy transformation of a falling object elegantly showcases the principle of conservation of energy. From potential to kinetic, the process illustrates a fundamental characteristic of nature. With knowledge comes responsibility; understanding these principles equips individuals to make informed choices that benefit both themselves and the environment. The next time you witness a falling object, take a moment to appreciate the magnificent interplay of energy at work, and challenge yourself to consider how you can contribute to the sustainable management of our resources.