The conservation of mechanical energy is a fundamental principle in physics that elucidates how energy behaves within isolated systems. The term ‘mechanical energy’ describes the sum of potential energy (PE) and kinetic energy (KE) present in an object. Understanding this concept opens a window to the intricate mechanisms underpinning physical phenomena, and it also illustrates the broader implications for energy conservation in our world.
To delve into the essence of mechanical energy conservation, one must first understand the individual components of mechanical energy. Potential energy is the stored energy of an object based on its position or configuration. For instance, an elevated rock possesses gravitational potential energy due to its height above the ground. Conversely, kinetic energy is the energy an object has due to its motion. The faster an object moves, the greater its kinetic energy. The relationship between these two forms of energy is encapsulated in the equation:
KE = ½ mv²
where ‘m’ represents mass and ‘v’ denotes velocity. Each form of energy interconverts as systems evolve, a topic that captivates many who study physics.
The principle of conservation of mechanical energy posits that in an ideal isolated system, where no external forces such as friction or air resistance intervene, the total mechanical energy remains constant throughout an object’s motion. Mathematically, this can be expressed as:
PE_initial + KE_initial = PE_final + KE_final
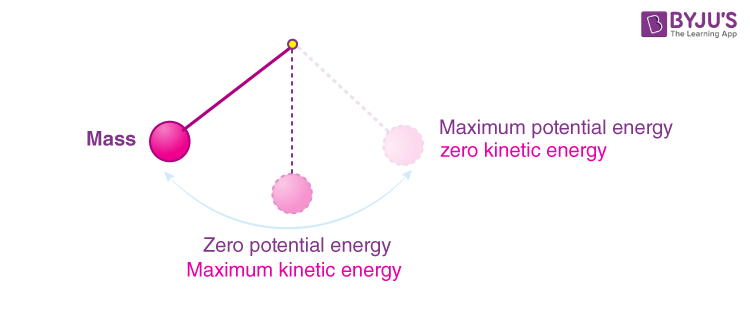
For instance, consider a pendulum swinging in a vacuum. At the apex of its swing, its velocity is zero; hence, its kinetic energy is nil, and its potential energy reaches a maximum. As it descends, potential energy transforms into kinetic energy, increasing its speed. At the lowest point of the swing, potential energy is at a minimum while kinetic energy is maximized. As the pendulum ascends again, kinetic energy transforms back into potential energy, emphasizing a continuous exchange that reflects the conservation principle.
This intriguing oscillation prompts deeper contemplation: Why does nature adhere so rigorously to these principles? The answer lies in the fundamental interactions of forces and energy. In practical scenarios, while external forces can dissipate energy—turning it into heat or sound—the isolated conditions of idealized systems pave the way for elegant explorations of energy dynamics.
The notion of mechanical energy conservation can also be applied to understand various phenomena observed in the natural world. For example, roller coasters rely heavily on this principle. At the peak of the initial climb, potential energy accumulates as riders gain altitude. As they descend, this energy transforms into kinetic energy, propelling the cars downward at thrilling speeds. The cyclic nature of energy exchanges within roller coasters is a vivid illustration of the conservation of mechanical energy in action.
Moreover, conservation of mechanical energy principles can extend far beyond theoretical physics and recreational activities. They have practical applications in various fields, including engineering, environmental science, and renewable energy technologies. Engineers design systems—be it in turbines, vehicles, or architectural structures—by accounting for these energy transitions to maximize efficiency and minimize energy loss.
For instance, in wind turbine technology, mechanical energy generated by wind motion is converted into electrical energy through the turbine’s rotational motion. Understanding and applying the conservation of mechanical energy principles allows engineers to optimize these conversions for sustainability, reducing our reliance on fossil fuels and minimizing ecological footprints.
This deeply ingrained connection between physics and environmental considerations raises stimulating inquiries into our societal energy choices. The continuous oscillation between potential and kinetic energy reminds us of the natural equilibrium that exists in systems striving for a state of energy efficiency. As environmental stewards, it is crucial to promote energy practices consistent with these principles. This can involve advocating for technologies that harness mechanical energy efficiently or scrutinizing the environmental costs of energy expenditures. By aligning human activities with the laws of physics, society can transition towards sustainable practices.
In summary, the conservation of mechanical energy stands as a pivotal concept in physics that not only fosters an understanding of energy interactions but also resonates with real-world implications. As mechanical systems transition between potential and kinetic energy, they enhance our comprehension of equilibrium and efficiency. The equation governing this conservation principle serves as a reminder of nature’s intricacies, beckoning us to explore the underlying patterns that govern our universe. Through ethical energy practices and innovations informed by these principles, there exists a pathway toward a more sustainable future, where the beauty of physics directly informs environmental activism and societal responsibility. By recognizing the importance of conserving mechanical energy, we can not only appreciate the elegance of physics but also work towards a more harmonious existence with our planet.