What Is Conservation of Mechanical Energy Equation? Breaking Down the Math

Have you ever wondered how a roller coaster stays in motion, soaring up and down with grace while defying gravity? This delightful journey through physics is beautifully explained by the conservation of mechanical energy. But what is this equation that governs such exhilarating rides and natural phenomena? In this discussion, we will dissect the conservation of mechanical energy equation, delve deep into its components, and unpack the mathematics underlying this profound principle.

At its core, the conservation of mechanical energy principle states that in a closed system, without any external work being performed, the total mechanical energy remains constant. This statement engenders a rich world of possibilities and applications in both theoretical and practical realms of physics.

Mechanical energy, as defined by physics, comprises two primary components: kinetic energy (KE) and potential energy (PE). Kinetic energy refers to the energy possessed by an object due to its motion, whereas potential energy is the energy stored in an object as a consequence of its position or configuration. The equation for mechanical energy conservation can thus be succinctly stated in mathematical form:

E_total = PE + KE

Throughout the course of any motion, the interplay between these two forms of energy is dynamic. For instance, let’s consider an object in free fall. As it descends, its potential energy, based on its height above the ground, diminishes; simultaneously, its kinetic energy increases as it accelerates towards the Earth. The remarkable aspect of this relationship is that the total mechanical energy remains constant, provided no external forces—like air resistance—are acting on it. This brings us to the mathematical representation at play.

Kinetic energy can be formulated mathematically using the equation:

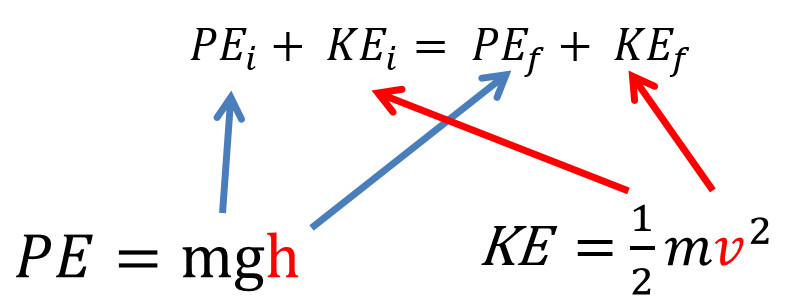
KE = 1/2 mv²

Here, m denotes mass, and v symbolizes velocity. As an object speeds up, its kinetic energy, as indicated by the square relationship to the velocity, increases dramatically. On the flip side, potential energy typically depends on gravitational forces and is represented as follows:

PE = mgh

In this equation, g represents the acceleration due to gravity (approximately 9.81 m/s² at Earth’s surface), and h indicates height above a reference point.

Now, armed with these foundational equations, let’s explore how they converge into one cohesive idea: the conservation of mechanical energy.

In an ideal scenario devoid of friction or air resistance, the initial mechanical energy (E_initial) will equal the final mechanical energy (E_final). Mathematically, this can be expressed as:

PE_initial + KE_initial = PE_final + KE_final

This relationship manifests beautifully when analyzing a pendulum swinging from its highest point to the lowest and back again. At the peak of its swing, the pendulum possesses maximum potential energy and minimal kinetic energy. As it descends, potential energy transforms into kinetic energy, peaking at the bottom of the swing. Here, one wonders: what happens to this energy during real-world applications where energy losses seem inevitable?

In practical scenarios, the conservation of mechanical energy is sometimes disrupted by non-conservative forces like friction and air resistance. These forces dissipate energy, rendering the total mechanical energy no longer conserved. Yet, even with these losses, the concept proposes challenges that remain meaningful—how can we minimize energy wastage in mechanical systems? Understanding the intricate dance of energy transformations can lead to innovative engineering solutions, improving efficacy in machines and everyday technology.

To illustrate this point, let us contemplate a classic example—the roller coaster. As the ride ascends a hill, work is done against gravitational force, resulting in significant potential energy. As the coaster plunges down, this potential energy translates into kinetic energy. Should we ignore the inefficiencies of friction and air drag, the total energy in the system is conserved. However, should engineers factor in these realities, energy loss must be meticulously calculated to optimize design and enhance rider experience.

To comprehend the practical implications of mechanical energy conservation, one must also explore energy transformation in various domains of life. Renewable energy, for instance, capitalizes on harnessing natural energy sources, transforming wind or solar energy into electrical energy while maintaining mechanical efficiencies. This understanding reveals a clearer path toward sustainability—by grasping energy conservation principles, we can improve renewable technologies, reduce energy consumption, and champion greener solutions.

In essence, the conservation of mechanical energy equation offers an indispensable lens through which to examine myriad phenomena, from the predictable rhythms of pendulum motion to the intricate designs of advanced machinery. It invites both students and professionals alike to engage playfully with physics, presenting opportunities for innovation and reflection on our energy practices. How will you utilize this fundamental concept to bolster your understanding of energy efficiency and contribute to a more sustainable future?

As we reflect on the significance of this principle, consider the relationships and applications that emerge not solely in theoretical discussions but also in proactive, real-world endeavors. By embracing the tenets of mechanical energy conservation, we pave the way for a more energy-conscious society, inspiring future generations to innovate and preserve our natural resources.