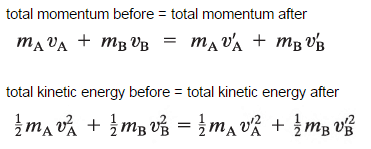Understanding the dynamics of physical interactions is essential for both academic inquiries and practical applications within the realms of physics and engineering. Two fundamental principles govern these interactions: the conservation of momentum and the conservation of energy. Although they frequently appear in tandem in problem-solving scenarios, their applications vary considerably depending on the circumstances. This article elucidates the criteria for applying each principle, enhancing your comprehension of these pivotal concepts.
Conservation of Momentum: The Catalyst of Collision Dynamics
The principle of conservation of momentum states that the total momentum of an isolated system remains constant when no external forces act upon it. Momentum is defined as the product of an object’s mass and its velocity. Thus, understanding this principle is crucial, particularly in situations involving collisions.
Inelastic vs. Elastic Collisions: Drawing the Distinction
To effectively apply the conservation of momentum, one must differentiate between elastic and inelastic collisions. An elastic collision is one in which both kinetic energy and momentum are conserved. These types of collisions typically occur at the molecular level, such as gas particles colliding. In contrast, inelastic collisions involve the conversion of kinetic energy into other forms—heat, sound, or deformation—resulting in a loss of kinetic energy, although momentum is still conserved.
Real-world scenarios where momentum conservation is essential include sports accidents or vehicle collisions. For instance, analyzing a car crash requires an understanding of momentum transfer between colliding vehicles. In such cases, computing the pre-collision and post-collision velocities using momentum conservation equations yields insights into the forces at play during the impact.
Implications in Engineering and Safety
The conservation of momentum has profound implications in engineering fields, particularly in analyzing crash safety in automotive design. By understanding how momentum distributes during a crash, engineers can innovate safer designs that dissipate energy effectively. This principle plays a vital role in developing crumple zones, safety barriers, and other protective measures to mitigate the consequences of high-speed collisions.
Conservation of Energy: The Guardian of System Dynamics
Unlike momentum, which is strictly a vector quantity, energy is a scalar quantity that cannot be created or destroyed, only transformed from one form to another. The principle of conservation of energy is pivotal when assessing dynamic systems, enabling predictions about the total system energy—including kinetic, potential, and thermal energy—in a closed environment.
Kinetic and Potential Energy: Unraveling the Energy Landscape
The conservation of energy principle flourishes in various scenarios, especially when examining mechanical systems. In such contexts, it elucidates interactions between kinetic and potential energy. For instance, a swinging pendulum epitomizes the transformation between potential energy at its peaks and kinetic energy at its lowest point. An intimate understanding of these transformations assists in solving complex problems in physics and engineering, providing insight into energy efficiency.
Thermal Dynamics and Energy Exchange
Additionally, the conservation of energy principle finds relevance in thermodynamic processes. When heat is exchanged within a system, understanding the energy transformations can guide engineers in designing more efficient systems, be they engines, refrigerators, or power plants. In analysis, one ascertains that the total energy before any process is equal to the total energy after, allowing for effective troubleshooting and optimization.
Strategic Application: When to Choose Momentum or Energy Conservation
Determining the appropriate principle to apply hinges on the specific conditions and characteristics of the system under scrutiny. The choice is vital, as using the wrong principle can lead to erroneous conclusions.
Utilizing Momentums in High-Impact Scenarios
Momentum conservation is particularly advantageous in high-impact scenarios involving collisions, explosions, or interactions where external forces are negligible. In these cases, focusing on momentum provides insights into the forces exerted during the event and the resulting motion.
Employing Energy Conservation for System Analysis
Conversely, energy conservation becomes paramount in analyzing systems where external forces are prevalent, or transformations occur. This includes assessing the efficiency of energy transformations in everyday applications, such as calculating the energy output of a wind turbine or a hydroelectric dam. By employing energy conservation principles, one can gauge performance and sustainability metrics.
Final Thoughts: Bridging the Two Principles
In conclusion, both conservation of momentum and conservation of energy are foundational principles in understanding physical interactions—each serving distinct purposes based on the nature of the interaction at play. Mastering the timing and context of each principle not only enhances academic prowess but also equips practitioners with critical understanding for real-world applications in engineering, environmental science, and technology development. Recognizing when and how to implement these principles will empower individuals to navigate the complexities of dynamics more effectively, fostering innovation and progress in various fields.