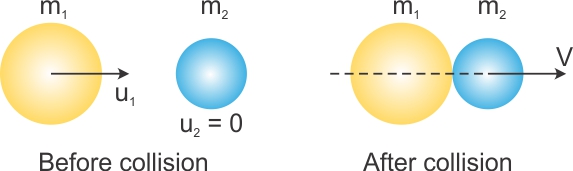
In the realm of physics, collisions are a fundamental aspect of studying motion and energy transformations. Among these collisions, inelastic collisions stand out for their unique characteristics. In an inelastic collision, two objects collide and do not rebound off each other, instead they may stick together, resulting in a loss of kinetic energy. This brings us to a critical question that resonates within the scientific community: Is energy conserved in inelastic collisions? Understanding the nuances of energy transformation in such interactions unveils a deeper insight into the principles governing our physical world.
Key to unraveling the answer is recognizing that while momentum is conserved in inelastic collisions, kinetic energy is not. This divergence sparks curiosity and prompts an exploration of how energy is redistributed during such events. The following sections delve into the mechanics of inelastic collisions, the nature of energy conservation, and the implications of energy transformation.
Understanding The Mechanics of Inelastic Collisions
Inelastic collisions can be conceptualized through various real-world scenarios; from car crashes to football tackles, the dynamics involved are pervasive in everyday life. When two objects collide inelastically, they experience a deformation and produce sound, heat, and sometimes even light. Unlike elastic collisions, where two separate entities retain their kinetic energy and can bounce apart, inelastic collisions are characterized by a shared fate. After the collision, the objects may move together as a single mass, thus altering their trajectories and velocities.
The mathematical representation of momentum conservation provides clarity in this scenario. For two objects, say object A and object B, with masses mA and mB, and initial velocities vA and vB, the law of conservation of momentum states:
mA * vA + mB * vB = (mA + mB) * vfinal
This equation evidences the conservation of momentum. Yet, when we delve into kinetic energy, the story diverges sharply. Kinetic energy, given by the formula KE = 1/2 * m * v2, transforms peculiarly during an inelastic collision.
The Loss of Kinetic Energy: A Crucial Insight
The crux of the inelastic collision phenomenon is the transformation of kinetic energy into other forms of energy. The significant loss in kinetic energy can be attributed to factors such as inelastic deformation, thermal energy, and sound production. During the impact, some kinetic energy is absorbed by the materials involved, causing permanent deformation. For example, when two cars collide, the crumpling of metal absorbs an immense amount of energy, resulting in a reduction in the overall kinetic energy after the collision.
Mathematically, we can express the initial and final kinetic energies:
Initial KE = 1/2 * mA * vA2 + 1/2 * mB * vB2
Final KE = 1/2 * (mA + mB) * vfinal2
Upon evaluating the values, it becomes apparent that Initial KE > Final KE. The difference in these values quantifies the energy converted into sound, heat, or structural deformation—echoing the transformation of energy which occurs in the inelastic scenario.
Broader Implications of Energy Transformation
The recognition that kinetic energy is not conserved during inelastic collisions prompts broader implications in various fields, from automotive safety design to ecological considerations in energy use and efficiency. In the automotive industry, understanding energy transformation allows engineers to design vehicles that not only withstand collisions better but also enhance passenger safety by distributing kinetic energy more effectively. Through materials that crumple in a controlled manner, the goal is to absorb as much energy as possible during an impact, minimizing injuries.
Moreover, from an environmental standpoint, the principles of energy conservation and transformation challenge our understanding of sustainability. When energy is not conserved in its initial form, it hints at wasted energy that does not return to a useful state. This observation can be employed to foster innovations in energy-efficient systems and practices in both industrial applications and everyday routines.
The exploration of energy conservation in inelastic collisions also raises philosophical inquiries about the nature of energy itself. Is energy ever truly lost, or is it merely transformed? Such reflections promote a newfound wonder about the interconnectedness of energy systems within our universe, revealing layers of complexity that evoke curiosity and inspire further inquiry.
Conclusion: A Paradigm Shift
In sum, the study of inelastic collisions serves as a microcosm of the complexities surrounding energy interactions. While momentum remains a steadfast law, the transformation of kinetic energy during an inelastic collision challenges conventional notions of conservation. This sparks a shift in perspective—from a rigid understanding of energy as simply conserved to an appreciation of its dynamic nature. As we navigate the intricacies of energy transformations, we are invited to consider broader applications, enhance technological advancements, and cultivate a deeper respect for the energy systems that underpin our reality. Through this exploration, a rich tapestry of knowledge unfolds, beckoning the curious and the environmental steward alike to contemplate the implications of energy in our world.