Understanding whether mechanical energy is conserved in a system is a fundamental aspect of physics that concerns many fields, from engineering to environmental science. Mechanical energy is defined as the sum of potential and kinetic energy in a system. It remains crucial to determine whether this energy remains constant, particularly in practical applications such as machinery design, energy efficiency evaluations, and environmental impact assessments. This guide elucidates how to ascertain whether mechanical energy is conserved, highlighting key factors and methodologies to identify these conditions.
Recognizing the essential components of mechanical energy requires an appreciation of potential and kinetic energy. Potential energy, often associated with gravitational fields, represents the stored energy of an object due to its position or configuration. Kinetic energy, on the other hand, relates to the energy an object possesses due to its motion. The principle of conservation of mechanical energy states that if no non-conservative forces (like friction or air resistance) perform work on a system, the total mechanical energy remains constant throughout the motion of the object.
In evaluating the conservation of mechanical energy, it is vital to identify the system’s boundaries and the forces acting on it. When analyzing a system, consider the following factors:
System Boundaries and Forces in Play
Defining the boundaries of the system under investigation is critical. Is the system isolated, or are external forces at play? In an isolated system where only conservative forces operate—such as gravitational or elastic forces—mechanical energy conservation is often upheld. However, if non-conservative forces, such as friction or air resistance, intervene, mechanical energy will decrease over time due to the conversion into thermal energy or sound.
To determine whether mechanical energy is conserved, one should:
- Identify the forces acting on the object within the defined boundaries.
- Assess if any external work is being done, either positively (adding energy) or negatively (removing energy).
- Count the types of energy present in the system, specifically looking for changes in potential energy, kinetic energy, and non-conservative energy losses.
Work-Energy Principle: The Connection Between Work and Energy Conservation
The work-energy principle provides a direct relationship between the work done by forces on an object and the change in its mechanical energy. If the net work done on the system is zero, mechanical energy remains constant. Conversely, if work is being done by non-conservative forces, such as friction, it signifies that energy is being lost from the mechanical energy framework.
To implement this principle effectively, document the forces acting on the system and calculate the work done. The work can be expressed as the force applied multiplied by the distance over which it is applied. Keep in mind that work done by non-conservative forces will decrease total mechanical energy. Therefore, it is essential to refine calculations by considering:
- The magnitude and direction of the forces.
- The displacement of the object along the direction of the force.
- Whether the system experiences a net loss or gain in mechanical energy.
Common Examples of Mechanical Energy Conservation
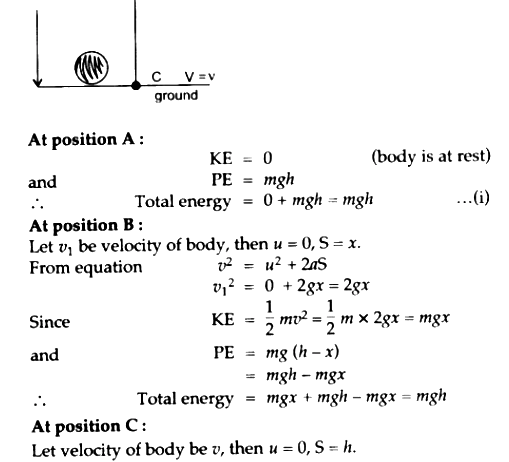
Understanding practical examples can illuminate the principle of mechanical energy conservation. In cases where an object is dropped from a height, its potential energy diminishes, while its kinetic energy increases proportionally until it impacts the ground; here, if it is assumed that air resistance is negligible, mechanical energy remains conserved. Similarly, in a pendulum, energy oscillates between kinetic and potential forms, illustrating mechanical energy conservation in an ideal environment free from resistance.
Another excellent case to examine is roller coasters. At the apex, the cars have maximum potential energy and minimum kinetic energy. As they descend, potential energy converts to kinetic energy, reaching maximum speed at the lowest points. Here, if we ignore friction and air resistance for simplicity, mechanical energy remains conserved throughout the ride.
Real-World Implications of Non-Conserved Mechanical Energy
In practical applications, ensuring mechanical energy conservation is vital for efficiency and sustainability. Machines with high mechanical energy loss due to friction often require more energy input, raising operational costs and decreasing overall efficiency. This aspect becomes critical in engineering designs where energy efficiency is paramount, such as in automotives and large machinery.
However, not all systems can achieve mechanical energy conservation, especially those involving non-conservative forces. In environmental contexts, understanding energy losses can inform the development of green technologies or sustainable practices that maximize energy efficiency and minimize waste. This awareness leads to improved designs and innovations across various sectors.
Conclusion: Assessing Mechanical Energy Conservation
In summary, determining if mechanical energy is conserved involves careful consideration of the forces at play within a system, the work being done, and understanding the transitions between potential and kinetic energy. With a thorough grasp of these components and practical knowledge of examples, one can clearly identify situations where mechanical energy is retained or lost. This understanding is paramount for engineers, physicists, and environmentalists seeking to create efficient systems and mitigate energy waste in a rapidly changing world.