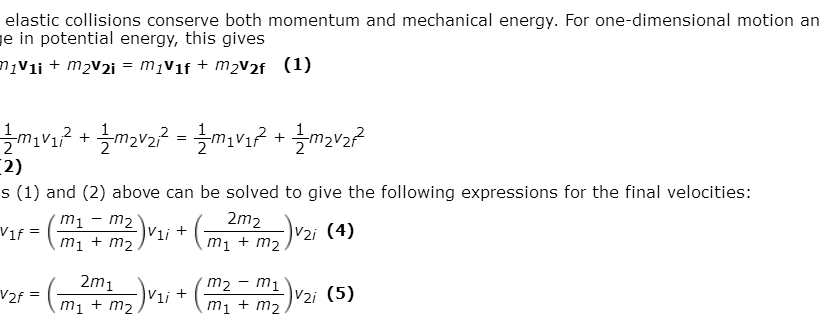When discussing the fundamental principles of physics, the notion of elastic collisions emerges as a cornerstone in the study of momentum and energy conservation. This phenomenon plays a critical role in various natural processes and engineered systems, ranging from molecular interactions to celestial mechanics. A pressing question often arises: do elastic collisions conserve kinetic energy? This inquiry not only addresses the mechanics involved but also clarifies how energy behaves during these interactions, establishing a foundation for several practical applications.
Understanding elastic collisions requires a thorough exploration of certain physical concepts, namely momentum and kinetic energy. Momentum, defined as the product of an object’s mass and its velocity, retains its value before and after a collision in an isolated system. Kinetic energy, on the other hand, is the energy an object possesses due to its motion, calculated using the formula KE = ½ mv². Distinguishing between elastic and inelastic collisions is pivotal, as the former entails the complete conservation of kinetic energy, while the latter results in a loss of energy in the form of sound, heat, or deformation.
Before delving deeper into the nuances of elastic collisions, it is essential to outline the characteristics that define them. An ideal elastic collision is characterized by two criteria:
1. Both kinetic energy and momentum of the colliding bodies are conserved.
2. The bodies involved do not exhibit any permanent deformation or generation of heat.
These ideal conditions are rarely encountered in real-world scenarios; however, understanding them provides a valuable framework for analyzing and interpreting a broad spectrum of physical phenomena.
The Mechanics of Elastic Collisions
Within the scope of classical mechanics, elastic collisions can be analyzed using both one-dimensional and multi-dimensional frameworks. In a one-dimensional elastic collision, two objects approach each other with known velocities and masses. Upon collision, they rebound, and their velocities after the impact can be calculated using equations derived from the conservation laws of momentum and kinetic energy. For instance, if two identical masses collide, they will exchange their velocities if one is stationary and the other is moving. This elegant interplay demonstrates the notion that momentum is conserved through an exchange of energy rather than an absolute retention of each body’s initial kinetic energy.
The complexities deepen in two-dimensional elastic collisions. When two bodies collide at angles, it is imperative to break down the velocities into their vector components to perform meticulous calculations. Understanding the angles of deflection is essential and leads to the application of trigonometric identities to determine directional changes post-collision. This multi-dimensional aspect amplifies the challenges, yet it also mirrors more intricate interactions in nature, such as the behavior of particles in gaseous states or the movements of celestial bodies.
Real-World Applications: Elastic Collisions in Everyday Life
While the theoretical framework may be fascinating, the practical implications of elastic collisions are widespread and significant. Numerous applications across various fields rely on the principles of elastic collisions for efficiency and effectiveness. For example, the design of sports equipment, such as billiard balls, relies on maximizing elastic collisions to ensure minimal energy loss in gameplay. The outcome of each shot and the dynamics between the balls are contingent upon their ability to conserve energy during impact.
In the automotive industry, the design of crumple zones in vehicles contradicts the principles of elastic collisions, as they are purposely engineered to absorb energy during an impact rather than conserve it. This illustrates that while elastic collisions dominate the theoretical framework, inelastic collisions play an equally crucial role in enhancing safety.
Another noteworthy application of elastic collisions is found in astrophysics. Stellar collisions, particularly in binary star systems, offer insight into the energy exchanges that dictate orbital dynamics and the eventual fates of stars. The study of such interactions has profound implications on our understanding of the universe, from formation theories to the life cycles of stars.
Considerations in Energy Conservation
One of the key concepts surrounding elastic collisions is the paradox of conservation of energy. Despite the complexities often associated with real-world collisions, in ideal conditions, kinetic energy remains conserved, reinforcing the law of conservation of energy. Inelastic collisions, however, often lead to disparities in kinetic energy, manifesting the reality that energy is not lost but transformed into other forms.
It is essential to comprehend that while many physical collisions may not achieve perfect elasticity, the insights gained from studying them provide valuable knowledge for innovative technologies and sustainable practices. By understanding how energy behaves across different types of collisions, engineers and scientists can create more efficient systems, whether it be in renewable energy technologies, manufacturing processes, or infrastructure developments.
Conclusion: The Intricacies of Elastic Collisions
In summation, elastic collisions succinctly illustrate the interplay between momentum and kinetic energy conservation. By unraveling the mechanisms behind these collisions, one can grasp a broader understanding of energy behavior in various contexts. Although perfect conditions may remain an idealization, the principles derived from studying elastic collisions have immense applicability across scientific disciplines and daily life. Understanding these principles not only enhances our comprehension of physics but also informs future advancements aimed at harnessing energy with greater efficacy. Through continued exploration of elastic collisions and their variants, the path to innovative solutions and sustainable practices becomes clearer, highlighting the perpetual relevance of classical mechanics in our modern world.