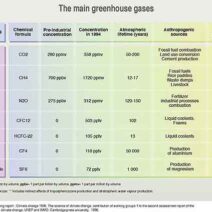
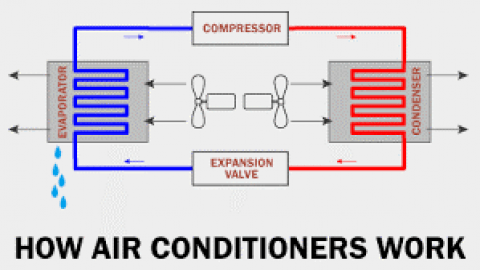
Understanding the dynamics of kinetic energy in the realm of physics necessitates an exploration of elastic collisions. Differentiating between types of collisions is fundamental for grasping how kinetic energy behaves under various conditions. In essence, the question arises: Is kinetic energy conserved during elastic collisions? This article endeavors to elucidate the intricacies of energy conservation within this context.
Before delving into the topic, it is imperative to define what is meant by elastic collisions. An elastic collision is characterized by the conservation of both kinetic energy and momentum. When two bodies collide elastically, they not only rebound off each other but do so without any loss in energy due to deformation or heat. An appropriate analogy might be two billiard balls striking each other on a pool table; they bounce back with their total energy intact.
Conversely, inelastic collisions result in the dissipation of kinetic energy. For example, when two cars collide at an intersection and become entangled, kinetic energy is transformed into other forms of energy, primarily sound and thermal energy. Thus, discerning these distinctions is essential when considering the conservation of kinetic energy.
To better understand the principle of conservation in elastic collisions, we must first familiarize ourselves with the laws of physics governing these interactions. The foundation is based upon the conservation equations, which assert that the total momentum before and after the collision remains constant, as does the kinetic energy.
A critical element in exploring kinetic energy is the equation derived from classical mechanics:
Kinetic Energy (KE) = 1/2 mv²
In this formula, ‘m’ denotes mass and ‘v’ signifies velocity. During an elastic collision, the total kinetic energy pre-collision equals the total kinetic energy post-collision. This principle underscores the essence of elastic collisions, making them a significant focus in the study of mechanics.
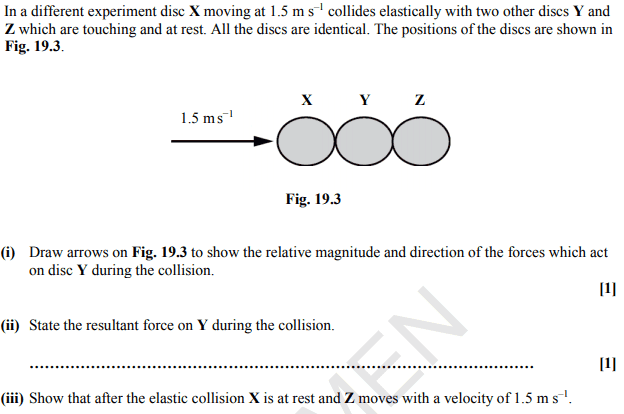
To fully grasp energy conservation in this context, consider that within an elastic collision, all participating bodies exchange their velocities without any conversion to thermal or potential energy. By analyzing simple systems such as two identical masses colliding elastically, one can effortlessly observe the conservation of kinetic energy.
Imagine two identical masses, each moving toward one another at equal speeds. Upon colliding, they exchange velocities, returning to their original states following the principles of momentum conservation. Each mass retains its original kinetic energy—evidencing that kinetic energy indeed remains conserved.
However, the beauty of elastic collisions extends beyond elementary systems; examining more complex scenarios can also reveal fascinating insights. For instance, when colliding non-equal mass objects, the conservation of kinetic energy is still maintained, albeit with differing post-collision velocities and trajectories. Mathematical relationships can be formulated to describe these outcomes, often leading to intriguing results in fields like astrophysics.
Furthermore, the notion of elastic collisions extends into everyday phenomena, including sports, automotive safety designs, and various engineering applications. In sports like volleyball or basketball, the elasticity of the balls directly affects performance. Manufacturers continue to optimize materials that bolster energy retention upon impact, enabling higher rebounds and greater speeds.
In the automotive sector, safety mechanisms like crumple zones come into play. While ideally, collisions should account for elastic behavior, the reality involves managing energy dissipation to minimize human injury. These engineered zones are vital for minimizing the kinetic energy not conserved during a collision by redirecting energy efficiently, thus protecting passengers.
Consequently, discussions surrounding kinetic energy conservation ignite more profound philosophical inquiries as well. In a universe composed of kinetic exchanges, what implications does conservation have on our understanding of energy and motion? As we probe deeper, awareness grows that while energy may oscillate between forms, the balances retain structural integrity—a principle echoed from molecular dynamics to cosmic interactions.
Despite the excitement surrounding elastic collisions, it remains integral to recognize the role of inelastic collisions in the grand tapestry of physics. Here, significant energy transformations occur, highlighting fascinating phenomena—a collision, for example, may transform kinetic energy into potential energy, leading to additional considerations in energy conservation equations.
Ultimately, the examination of elastic collisions and the conservation of kinetic energy unveils a complex interplay of physics, engineering, and real-world applications. It serves as a reminder of the intricate dance between energy forms—a principle that governs not only the behavior of colliding bodies but also the very fabric of our universe.
In summary, the exploration of kinetic energy in elastic collisions provides a cornerstone for grasping broader concepts in physics and engineering. By acknowledging and analyzing both kinetic and potential transformations, a comprehensive understanding of energy conservation emerges—a critical pillar in the ongoing quest to unravel the mysteries of motion and energy in nature.