The principle of mechanical energy conservation is a cornerstone in the realms of physics and engineering. It holds significant relevance in countless real-world situations. But what does it really mean? When is mechanical energy conserved? And are there scenarios where this principle may not apply? Let us embark on an enlightening expedition through the concept of mechanical energy and the circumstances under which it remains unchanged.
The term “mechanical energy” encompasses two main components: kinetic energy and potential energy. Kinetic energy is the energy a body possesses due to its motion, while potential energy is the energy stored in an object due to its position or configuration. The law of conservation states that in the absence of external forces, the total mechanical energy of an isolated system will remain constant. This sets the stage for numerous implications and applications in various fields.
Have you ever wondered about the elegance of a child swinging on a playground swing? As the child swings higher, her potential energy increases, while her kinetic energy decreases at the apex of the swing. At the lowest point of the swing, the reverse occurs—kinetic energy reaches its peak while potential energy wanes. This interplay illustrates a classic scenario in which mechanical energy is conserved. The system, in this case, is isolated from external forces like friction or air resistance, allowing the total mechanical energy to remain unchanged.
However, our exploration does not end here. There are several domains where the conservation of mechanical energy holds true, and they often hinge upon specific conditions. Below, we delve deeper into the noteworthy scenarios where mechanical energy is consistently conserved.
In a frictionless environment, mechanical energy conservation reigns supreme, often idealized in physics problems. Consider a frictionless pendulum. As it swings from one side to the other, it exemplifies the cyclic transformation between kinetic and potential energy. Here, no external forces act on the pendulum, affirming that its total mechanical energy remains constant throughout the motion, leading to a graceful dance of energy conversion.
An equally enchanting scenario unfolds in the realm of conservative forces. These forces, such as gravitational force, have a remarkable property—work done by these forces on an object depends only on the initial and final positions, not the path taken. For instance, in the case of an object being dropped from a height, gravitational force is a conservative force. As the object descends, its potential energy converts into kinetic energy, all while the total mechanical energy remains unaltered. Such phenomena occur in systems interacting solely through conservative forces, heralding another situation of energy conservation.
Yet, the equilibrium we observe is delicate. As we expanding our understanding of mechanical energy, we encounter scenarios where conservation does not apply. Consider external forces like friction. A classic example is a roller coaster. When the coaster climbs an incline, mechanical energy decreases due to frictional forces resisting motion. Energy is dissipated as thermal energy, and the system does not conserve total mechanical energy as external forces alter its state.
Similarly, real-world applications often involve conversions of mechanical energy into other forms. Take a car navigating through a winding road. As the car accelerates downhill, potential energy converts to kinetic energy. However, external forces such as friction and air resistance siphon off valuable energy, preventing the mechanical energy from remaining constant. This highlights the complexities of energy conservation in everyday applications.
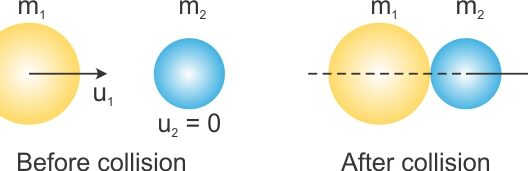
Another captivating case arises in elastic collisions, offering insight into the conservation of mechanical energy aspect. In an ideal system with no external forces and perfectly elastic collisions, mechanical energy is conserved. Imagine two billiard balls colliding on a frictionless table; their mechanical energy before the impact equals the total mechanical energy post-collision. Contrast this with inelastic collisions where kinetic energy is transformed into other forms of energy, thereby altering the mechanical energy within the system. This illustrates how the type of collision directly affects energy conservation.
As we ponder these scenarios, it becomes evident that while mechanical energy conservation is a fundamental principle, its application hinges on uncontested conditions. Factors such as the presence of external forces or the type of collision shape the dynamics of energy conservation. Recognizing these variables allows for deeper comprehension of the physical systems we encounter.
So, next time you witness a child on a swing or an athlete executing a high jump, consider the elegant interplay of energy at play. The universe operates in harmony, with mechanical energy shifting forms under the right conditions, yet revealing its limits under external influences.
In essence, exploring when mechanical energy is conserved can contribute significantly to our understanding of nature’s laws. As we dissect these scenarios, reflecting on the nuances of energy transformation enriches not only our grasp of physics but also our appreciation for the intricate systems that govern the world around us.