Understanding the principles of physics is instrumental in grasping the fundamental workings of the universe. Among these principles, angular momentum and energy conservation stand out, providing a clear lens through which to observe motion and dynamics not only in macroscopic environments but also at subatomic levels. As we unravel the complexities surrounding angular momentum conservation, an intriguing question arises: can angular momentum be conserved even when energy isn’t?
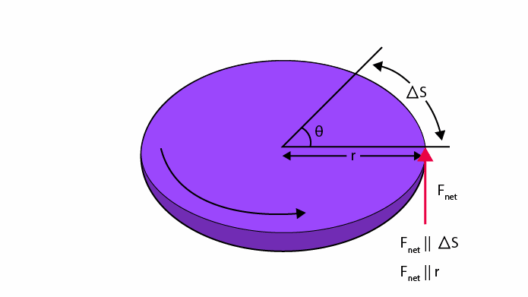
To explore this enigma, we must first dissect the concepts of angular momentum and energy. Angular momentum, denoted as (mathbf{L}), is a vector quantity that represents the rotational inertia and the angular velocity of an object. Formally, it can be expressed as the cross-product of the position vector (mathbf{r}) and the linear momentum (mathbf{p}): (mathbf{L} = mathbf{r} times mathbf{p}). This quantity is particularly vital when examining systems that involve spinning bodies, or particles in a rotating frame.
Energy, on the other hand, manifests several forms, such as kinetic and potential energy. The law of conservation of energy states that within a closed system, energy cannot be created or destroyed; it can merely change forms. This fundamental principle has been integral in various domains, from mechanical systems to thermodynamics.
The intersection of these two principles becomes particularly compelling in scenarios where external forces may do work on a system. Consider the case of a figure skater performing a spin. As they draw their arms in closer to their body, they rotate faster. This phenomenon is dictated by the conservation of angular momentum; the skater decreases their moment of inertia, which results in an increase in angular velocity to keep (mathbf{L}) constant. Here, energy transformations are apparent since kinetic energy changes due to the varying speed of rotation.
But what happens in systems where energy conservation does not hold? A quintessential example lies in inelastic collisions, where kinetic energy is transformed into other forms, such as heat, sound, or deformation. During these interactions, total energy is not conserved in its mechanical form, yet angular momentum can still be conserved under certain conditions. This principle is particularly significant in astrophysical phenomena, such as the dynamics of galaxies and the behavior of celestial objects during collisions.
Furthermore, consider a spinning disc thrown onto a surface without friction. The disc experiences no external torque, and thus, its angular momentum remains unaltered despite the energy dissipated from the system as sound or minor thermal energy. This represents a striking confirmation of the conservation of angular momentum occurring independently of energy conservation.
These principles find resonance in quantum mechanics, where phenomena become even more perplexing. In quantum systems, particles exhibit behaviors that defy classical intuition. Particle decays or scattering processes might involve changes in energy and particle states, yet angular momentum conservation remains sacrosanct. For instance, when two particles collide and produce a new particle, the total angular momentum of the system before and after the event must remain constant, even if the energy reflects a different balance in various forms.
This fabric of understanding prompts us to reconsider our perspectives on competition between various conserved quantities. One might often assume that the conservation laws must work hand-in-hand; yet, they can operate independently. The ability of angular momentum to remain conserved in scenarios of energy transformation invites us to rethink our preconceptions about dynamic systems.
Another plane where this disassociation becomes essential is in non-conservative forces. Systems subjected to external influences like air resistance or friction often witness a dissipation of energy, yet findings in those same systems show that angular momentum can still be conserved. For example, a spinning top eventually succumbs to the friction of the table, leading to a gradual loss of energy as it slows down. However, until the very moment it ceases to spin, its angular momentum remains constant if seen from the perspective of the forces acting on it.
The case of electric motors provides a concrete illustration of angular momentum and energy dynamics. When motors run, electrical energy is transformed into mechanical energy causing rotational motion. However, losses occur due to heat and friction, representing energy dissipation. Despite these losses, as long as the system is closed to external torques, angular momentum conservation prevails, thereby showcasing the coexistence of these two distinct kinds of conservation laws.
Thus, as we embrace the intricacies of physics, we uncover a nuanced understanding that embodies complexity and paradox. The ability of angular momentum to remain conserved in systems where energy conservation does not apply challenges our viewing lens of classical mechanics. Humans possess an insatiable curiosity that drives inquiry, enticing us to investigate further methodologies that probe these essential laws of nature.
This exploration into angular momentum and energy conservation comes at a pivotal moment, particularly when considering the ecological and engineering implications. As we shift towards sustainable sources of energy and strive to conserve our terrestrial resources, the physical underpinnings guiding our technologies deserve informed scrutiny. The principles encapsulated in discussions of angular momentum conservation can ignite innovative solutions, inspiring a deeper dialogue on how we exploit natural laws to engineer changes conducive to preserving our environment.
In conclusion, while angular momentum can indeed be conserved even when energy is not, this discovery engenders a realm of thought that transcends conventional wisdom. It encourages us to foster a perspective that embraces complexity, urging us to further delve into the rich tapestry of the universe’s governing laws. The interplay between these apparently disparate conservation principles stands as a testament to the intricacies of motion and energy in our lives and the cosmos at large.