Mechanical energy, the sum of potential and kinetic energy in a system, is a fundamental concept in physics. It captivates us because it embodies the elegance of energy transfer and conservation across various contexts, from the simple act of a ball being thrown to the complexities of celestial mechanics. However, mechanical energy is not always conserved. Understanding the conditions under which mechanical energy remains constant can illuminate the underlying principles governing physical interactions.
In an ideal world devoid of non-conservative forces, mechanical energy is indeed conserved. This idealization prompts us to explore when and why this conservation may not hold true. To appreciate the nuances of mechanical energy conservation, we must delve into the contexts in which it is applicable, the principles governing these contexts, and the implications for real-world systems.
Understanding the Dynamics of Energy Conservation
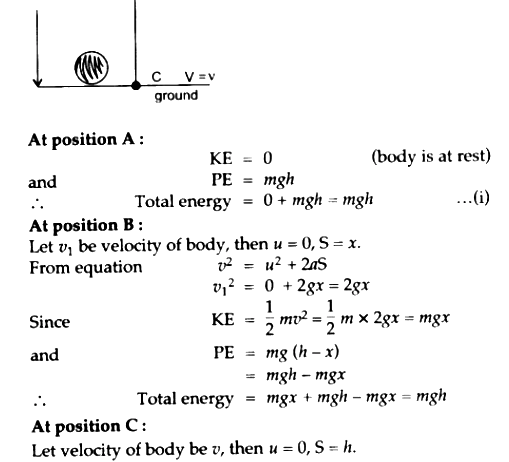
In mechanics, we often encounter closed systems, where external forces do not interfere. Within these systems, mechanical energy conservation is easily demonstrated. For example, when a pendulum swings, its mechanical energy oscillates between kinetic and potential forms, with the total energy remaining constant—assuming no air resistance or frictional forces act upon it. This illustrates the principle of conservation of mechanical energy: the energy is merely transformed from one type to another without any loss.
However, the introduction of non-conservative forces complicates the narrative. Friction and air resistance are prime examples of non-conservative forces that dissipate mechanical energy as thermal energy. As a consequence, while the total energy in a closed system remains conserved (as per the first law of thermodynamics), the mechanical energy diminishes. A classic illustration is a roller coaster: as the coaster climbs, it accumulates potential energy, which converts into kinetic energy as it descends. The mechanical energy, however, is less than expected due to energy loss to friction with the tracks and air resistance.
Recognizing these forces allows us to analyze various mechanical systems accurately. Conservative forces, such as gravitational and elastic forces, do not dissipate energy; rather, they store it and release it. The conservation law holds in any system governed exclusively by conservative forces, enabling us to predict the behavior of the system with remarkable accuracy.
The Building Blocks of Mechanical Energy
Potential and kinetic energy form the cornerstone of mechanical energy. Potential energy (PE) represents stored energy based on an object’s position or configuration. Gravitational potential energy, for instance, is given by the equation PE = mgh, where m is mass, g is the acceleration due to gravity, and h is height. Kinetic energy (KE), on the other hand, is the energy of motion described by KE = 1/2mv², with m as mass and v as velocity. When energy transitions between these two states, mechanical energy conservation is often at play.
An intricate part of this framework is the conservation of energy principle. It posits that energy cannot be created or destroyed; rather, it shifts forms. In isolated systems where only conservative forces function, mechanical energy remains conserved. This principle manifests in various scenarios—from a diver leaping off a platform to the gravitational interactions governing planetary orbits.
Moreover, the elegance of this conservation principle extends beyond simple mechanical systems. In thermodynamic contexts, even when mechanical energy dissipates, the total energy contained within the system continues to abide by the conservation laws. This universality enchants physicists and scholars, linking classical mechanics with broader energy principles.
Applying Conservation Principles in Real Life
While theoretical models elucidate conservation principles, real-life applications showcase the complexities influencing mechanical energy conservation. Engineers and architects harness these principles in designing structures and machinery ranging from bridges to amusement park rides. Understanding how energy transforms and dissipates informs safer and more efficient designs. For instance, a well-constructed roller coaster maximizes kinetic energy during thrilling drops, making the ride captivating while minimizing energy losses through friction.
Consider also the implications for ecological systems. In natural environments, energy dynamics play a substantial role in ecosystem sustainability. Plants convert solar energy into chemical energy through photosynthesis, exemplifying a direct application of energy transformation principles that align with mechanical conservation. Thus, understanding these energy dynamics extends into environmental stewardship, emphasizing the interconnectedness of energy principles across all scientific fields.
Conclusion: The Fascination of Conservation
The exploration of mechanical energy conservation reveals a tapestry of principles interwoven with both theoretical elegance and practical applications. By recognizing the conditions under which this conservation holds true and acknowledging the disruptive influence of non-conservative forces, we gain deeper insights into not only mechanical interactions but also broader energetic systems. This knowledge fosters appreciation for both the intricacies of mechanical systems and the larger ecological picture, where energy conservation principles govern the balance of our natural world. Ultimately, the investigation of mechanical energy conservation is a window into the beauty of physical law, highlighting our fascination with the interplay between energy, motion, and the environment.