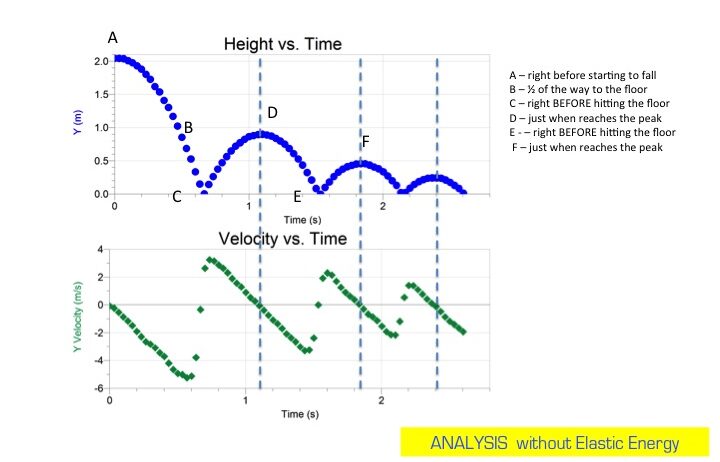
When analyzing the concept of energy conservation, one intriguing demonstration is the behavior of a bouncing ball. At first glance, it may appear simply as a recreational object; however, a closer examination reveals intricate physical principles at work. The question arises: does a bouncing ball exhibit conservative energy? This exploration delves into the nature of energy conservation, types of energy involved, and the indicative lessons derived from the motion of a bouncing ball.
To initiate the discussion, one must first understand what is meant by conservative energy. In physics, conservative energy pertains to systems where the total mechanical energy (kinetic plus potential energy) remains constant, assuming no dissipative forces such as friction or air resistance. This principle is vital for various applications in scientific fields ranging from engineering to environmental studies. The bouncing ball serves as an exquisite example to illustrate these concepts, revealing complex interactions between kinetic energy and gravitational potential energy.
When a ball is held at a certain height, it possesses gravitational potential energy due to its position in the Earth’s gravitational field. This energy is quantified by the formula:
PE = mghwhere PE is potential energy, m is mass, g is the acceleration due to gravity, and h is the height above a reference point. The higher the ball is raised, the more potential energy it acquires. Upon release, this potential energy begins its transformation as the ball accelerates downward. As it falls, the potential energy decreases while kinetic energy increases, described by the kinetic energy formula:
KE = 0.5mv²In this equation, KE is kinetic energy while v is the velocity of the ball. At the point just before impact with the ground, the ball reaches its maximum velocity and, consequently, maximum kinetic energy, as its potential energy nears zero. This energy transformation embodies the principles of energy conservation in an idealized, frictionless scenario.
However, in a real-world context, energy dissipation occurs. When the ball strikes the ground, it experiences an inelastic collision, where some kinetic energy is converted into other forms of energy, such as thermal energy and sound energy. These conversions illustrate the importance of understanding energy dissipation in systems involving external forces, revealing that not all the initial potential energy will be regained in the form of kinetic energy on the ball’s ascent.
When the ball rebounds, it ascends to a height less than its original height, revealing the interplay of conservative and non-conservative forces at work. The reduction in maximum height signifies energy losses, primarily through air resistance and deformation of the ball. This is where the notion of non-conservative forces becomes paramount. In practical scenarios, the energy does not fully return to the ball as mechanical energy, which could raise questions about its classification as a conservative energy system.
This phenomenon leads to the concept of the “bounce efficiency” of a ball. Highly elastic materials such as rubber can minimize energy loss, maintaining a more conservative behavior, whereas materials with greater inelastic properties would manifest pronounced dissipation. Accordingly, not all balls are created equal in terms of energy conservation. By examining the materials and structures of various balls, from rubber bouncy balls to heavy basketballs, one can discern significant differences in energy retention and bounce efficiency.
Moreover, the height achieved on subsequent bounces correlates directly with several factors: the initial height dropped from, the material of the ball, and the surface it impacts. Each variable introduces compelling insights into how energy is transformed, stored, and dissipated. For instance, a rigid surface allows for a more efficient transfer of energy, resulting in a more substantial rebound effect compared to a soft surface where energy dissipates as heat and deformation.
The implications of these energy transformations are extensive. They provide critical insight into broader phenomena in conservation and sustainability fields. Understanding energy conservation through a simple bouncing ball contributes to intricate topics such as renewable energy systems, where maximizing energy retention and minimizing waste is essential. It emphasizes the importance of material selection and design in creating efficient energy harnessing systems.
Furthermore, education plays a crucial role in promoting awareness about the principles of energy conservation. Simple experiments involving bouncing balls can engage individuals of all ages, enabling them to visualize and grasp complex scientific concepts. Such experiential learning fosters a deeper understanding of the importance of energy efficiency in daily life and larger environmental contexts.
In summary, the behavior of a bouncing ball offers a multifaceted exploration of energy conservation principles. While a ball’s motion appears simple, it embodies rich scientific themes surrounding energy transformation, conservation, and loss. Thus, a bouncing ball indeed illustrates the principles of conservative energy in theory, though practical realities introduce complexities that warrant consideration. By analyzing and understanding these dynamics, one can appreciate the significance of energy conservation and its foundational role in environmental sustainability and scientific inquiry.