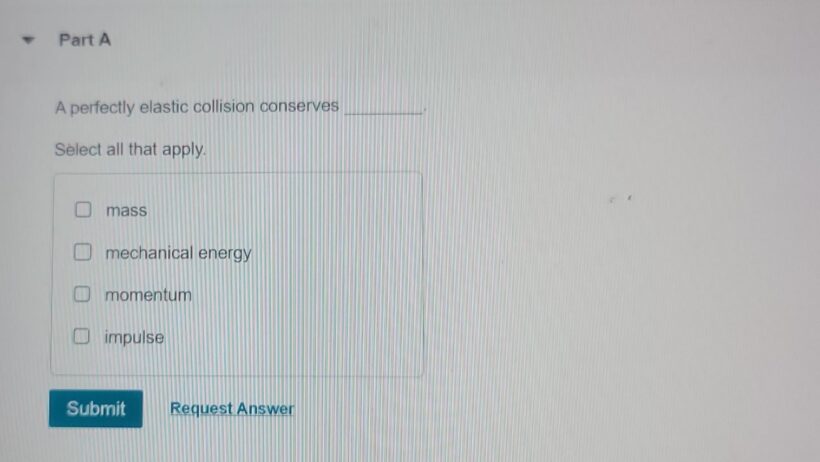
In the realm of physics, the investigation of collisions serves as a vital cornerstone for understanding fundamental principles, particularly within the context of mechanics. A question often pondered is whether a perfectly elastic collision conserves mechanical energy. This inquiry addresses a cornerstone observation in classical mechanics, revealing profound implications for both theoretical inquiry and practical applications.
To elucidate the concept of a perfectly elastic collision, it is imperative to define the term itself. A perfectly elastic collision is characterized by the complete conservation of kinetic energy and momentum. Within this framework, when two bodies collide, they rebound without any loss of kinetic energy, thereby endorsing the notion of perfect elasticity. This concept starkly contrasts with inelastic collisions, where kinetic energy is dissipated, transformed into other forms such as thermal energy or sound.
Symbolically, the conservation of momentum can be articulated as:
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
Here, m represents mass, u denotes initial velocity, and v signifies final velocity. For perfectly elastic collisions, this equation holds true alongside kinetic energy conservation, articulated as:
½m₁u₁² + ½m₂u₂² = ½m₁v₁² + ½m₂v₂²
Let us delve deeper into the implications of these equations. The first equation, the conservation of momentum, is universally applicable regardless of the nature of the collision. However, the fascinating aspect lies within the second equation; it commands our attention and elicits questions regarding the fundamental nature of energy in motion.
Why does kinetic energy remain intact during a perfectly elastic collision? To comprehend this phenomenon, one can consider the interplay of internal forces and external influences. In an isolated system, the sum of the kinetic energies of the interacting bodies remains unchanged. This implies an extraordinary symmetry in the forces exerted during the collision; the action and reaction are equal and opposite, a direct reflection of Newton’s Third Law.
However, the real enigma resides in the condition under which such perfect insulation from energy dissipation is achievable. In practice, while some collisions can be approximately elastic—think of atoms or particles in high-energy physics—most real-world collisions inevitably involve some degree of energy loss. The disparity between perfect theory and practical reality elicits a sense of fascination, underscoring the distinction between idealized models and empirical observations.
An energetic exploration of elastic collisions can be revealed through various practical applications. Consider the game of billiards, where understanding elastic collisions is crucial for executing precise shots. When the cue ball strikes another ball, if the collision is sufficiently elastic, the kinetic energy is conserved, enabling predictive models of motion based on the angles of impact. Such applications highlight not only the importance of theoretical models in real-world scenarios but also the intuitive grasp that human beings possess regarding motion, energy, and conservation laws.
Moreover, the intrigue of perfectly elastic collisions extends into the realm of astrophysics. Neutron stars, for example, create environments where the densities and gravitational forces yield interactions reminiscent of elastic collisions. These conditions allow astrophysicists to study the behaviors of matter under extreme states and contribute to a broader understanding of the universe. Herein lies a tantalizing intersection of theory and existence, where the very principles that dictate motion govern phenomena observable in the cosmos.
Nevertheless, while the concepts of momentum and energy conservation hold true in perfectly elastic collisions, real-world applications frequently introduce complexities. Factors such as friction, deformation, and sound energy can diminish the effectiveness of conservation laws as observed in practice. These deviations from the idealized model compel researchers to develop sophisticated models that can account for the nuances of real-life interactions. Each experiment reveals the limitations of theoretical constructs, while simultaneously illuminating paths for new inquiries and advances in scientific understanding.
Thus, we converge upon the profound realization that while perfectly elastic collisions theoretically conserve mechanical energy, actual conditions often diverge from this ideal caricature. Yet, this divergence does not diminish the significance of the concept; rather, it underscores a fundamental truth about the nature of energy and motion: the dance of particles and the intricacies of forces operate within a grand tapestry of physical laws.
In conclusion, the exploration of perfectly elastic collisions serves as a compelling investigation into the mechanics of energy, momentum, and the universe at large. While the conservation of mechanical energy is a salient feature of such collisions, reality presents an array of factors that complicate this idealization. Engaging with these complexities enhances comprehension, fostering a deeper appreciation for the subtleties of physics. The elegant balance of theory and practicality embodies the essence of scientific inquiry, inspiring both curiosity and further exploration into the intricate workings of our physical world.