Free fall is a phenomenon that captivates both the scientific community and the layperson alike, presenting a curious dance between gravity and inertia. When an object descends under the sole influence of gravitational force, it raises an intriguing query: does this process conserve mechanical energy? To unravel this question, we must delve into the fundamental principles of mechanical energy, the forces at play during free fall, and the implications for our understanding of energy conservation.
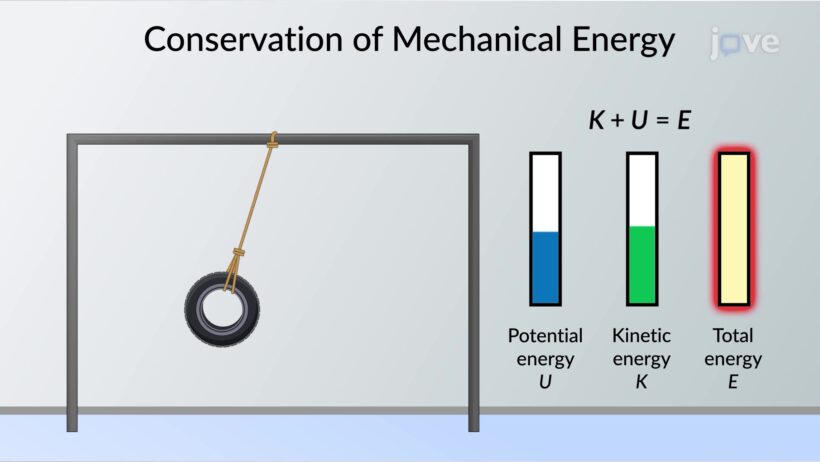
Mechanical energy is defined as the sum of potential energy (PE) and kinetic energy (KE). Potential energy, in the context of free fall, is the energy possessed by an object due to its height above a reference point, often the ground. As the object begins to descend, this potential energy will gradually convert into kinetic energy, which is the energy of motion. Mathematically, this is expressed as:
PE = mgh,
KE = 0.5mv².
Where m is mass, g is the acceleration due to gravity, h is height, and v is velocity. Initially, when an object is at rest at a height h, its kinetic energy is zero, and its potential energy is at its maximum. As it falls, it accelerates under gravity, increasing its velocity and thus its kinetic energy. At the moment just before it strikes the ground, the potential energy will have been entirely converted into kinetic energy, creating a state of equilibrium.
This transformation of energy adheres to the Principle of Conservation of Mechanical Energy, which states that in the absence of non-conservative forces, the total mechanical energy of a system remains constant. In the context of free fall, when we neglect air resistance and other forms of friction, the transformation from potential to kinetic energy occurs without a loss of total energy. Hence, it may appear that mechanical energy is indeed conserved during free fall.
However, in the practical world, air resistance plays a pivotal role. For objects falling through the atmosphere, air resistance acts as a force opposing the motion. This non-conservative force dissipates some of the mechanical energy into other forms, primarily thermal energy, resulting in a decrease in the total mechanical energy. Thus, while in an ideal vacuum, mechanical energy is conserved during free fall, the situation becomes more complex in the presence of air. This realization prompts a deeper exploration of energy forms and transitions.
Consider an object like a skydiver during a free fall. Initially, as they exit the aircraft, they experience a marked decrease in potential energy while simultaneously increasing their kinetic energy. However, as they accelerate, air resistance becomes significant, leading to a point known as terminal velocity — the state where gravitational force is balanced by drag force, leading to no net acceleration. At terminal velocity, the fall stabilizes, and the energy dynamics shift. The mechanical energy is conserved only to the extent that the energy is redistributed rather than entirely lost; it now appears as kinetic energy altered by the work done against air resistance.
This process can be visualized using energy bar charts that depict the transitions between potential and kinetic energy states at various moments during free fall. Such diagrams illuminate the relationship between height, velocity, and the energy transitions occurring throughout the descent. They highlight the exquisite balance of energies and the variables that might affect energy conservation, sparking curiosity and deeper contemplation.
What compels us to examine free fall so intently? The sight of an object plummeting through the atmosphere evokes visceral emotions. It taps into our primal instincts, reminding us of the forces of nature that govern our everyday lives. Despite its simplicity, free fall encapsulates fundamental principles of physics, demonstrating elegance through its predictability. This fascination intertwines with the notion of gravity as a universal force, shaping our understanding of the cosmos.
Moreover, the implications of understanding mechanical energy conservation extend beyond theoretical explorations. Engineering fields rely on these principles for safety applications like the design of parachutes and the mechanisms of various transport systems. Architectural designs consider gravitational effects, ensuring stability and structural integrity. Furthermore, insights from energy conservation lead us to enhance our energy efficiency, an increasingly pressing concern in our carbon-constrained world.
It is paramount to recognize the intersection between free fall, mechanical energy, and broader environmental concerns. As we interrogate energy conservation within physical systems, we simultaneously confront the necessity of employing these principles in energy conservation methodologies. Transitioning to renewable energy sources, enhancing energy efficiency in devices, and fostering sustainable practices all hinge upon our comprehension of energy principles.
In conclusion, the relationship between free fall and mechanical energy conservation presents a fascinating tableau rich with implications for both science and society. In a perfect environment devoid of friction, one could affirmatively claim that free fall conserves mechanical energy. However, in the pragmatic world filled with resistive forces, the conservation becomes nuanced, showcasing the intricate interplay of energy transformations. The fascination surrounding free fall serves as a reminder of the wonder of physics, a call to embrace our understanding of the natural world, while fostering a commitment to energy conservation for the benefit of our environment.