Explosions are a captivating spectacle, akin to a cosmic ballet where energy pirouettes through space and time. Yet, beneath their dramatic exterior lies a complex interplay of fundamental physical principles: momentum and kinetic energy. Understanding these concepts reveals why momentum is conserved in explosive events, while kinetic energy may not be conserved, opening a window into the mechanics of such startling phenomena.
To embark on this journey of exploration, we must first delineate the meanings of momentum and kinetic energy. Momentum, defined as the product of mass and velocity, is a vector quantity – it has both magnitude and direction. Kinetic energy, however, is a scalar quantity, representing the energy an object possesses due to its motion, mathematically expressed as one-half the mass multiplied by the square of its velocity. While they are related, the nuanced distinctions between the two concepts become particularly significant during explosive interactions.
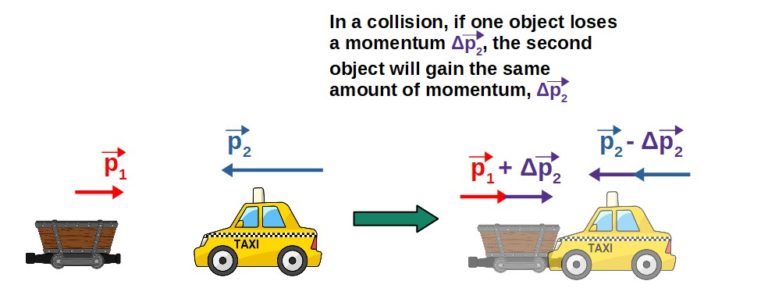
Imagine a firework bursting in the sky. As it detonates, the chemical energy stored within the explosive material transforms into kinetic energy, resulting in colorful sparks shooting outward in every direction. In this grand spectacle, we can observe the law of conservation of momentum in action. The total momentum of the system before the explosion must equal the total momentum after the explosion. In mathematical terms, this can be articulated as: the momentum before the event equals the momentum after the event.
This principle stands resolutely—independent of the type of explosion. For instance, consider two cars colliding. Before the crash, they both possess certain momentum. Upon impact, the forces exerted during the collision redistribute the momentum between the two vehicles, yet the total combined momentum remains unchanged. The outcome adheres to the stipulation that momentum is conserved in isolated systems, regardless of the myriad transformations that may occur during an explosion.
Conversely, kinetic energy reveals a more complex narrative. In the firework example, while momentum remains conserved, the kinetic energy disperses. An explosion causes a sudden release of energy that can create new forms of kinetic energy in the surrounding debris, which can alter the total kinetic energy in the system. Explosions frequently result in thermal energy, sound energy, and even structural deformation, causing kinetic energy before the event to be transformed rather than consistently conserved.
The disparities between momentum and kinetic energy conservation can often be illustrated through real-world scenarios. In a perfectly elastic collision, both momentum and kinetic energy are conserved, akin to two billiard balls bouncing off each other. However, in inelastic collisions—this includes many explosive events—momentum remains conserved, while kinetic energy dissipates as heat, sound, and fragmentation. Thus, one might think of momentum as the unyielding thread that links the initial and final states of a system, while kinetic energy metamorphoses like a fleeting shadow, unable to remain invariant through transformation and chaos.
Intriguingly, the distinction between conservation of momentum and kinetic energy can also be elucidated using metaphors. Picture a magician performing card tricks. The cards—like momentum—seem to adhere to the rules of magic; they appear, disappear, and transform, yet their total count remains constant. Meanwhile, the spectacle itself, with bright lights and elaborate props, represents kinetic energy. Some energy dissipates in the form of fireworks and applause; thus, despite the magic inherent in the show, the kinetic energy evaporates into different forms, similar to how it disappears in explosive reactions.
A case study that exemplifies this dichotomy can be found in the realm of nuclear physics. When a nucleus undergoes fission, it splits into smaller fragments, releasing vast amounts of energy. The total momentum of the nucleus is conserved throughout the process, but the kinetic energy varies dramatically due to the transformation into different energy forms. Such processes not only highlight the conservation of momentum but also the susceptibility of kinetic energy to creative vagaries.
Understanding these concepts has profound implications, particularly when addressing safety in explosive environments or designing controlled explosions, such as those found in mining or demolition. By calculating the momentum and understanding how kinetic energy dissipates, engineers can predict outcomes and mitigate potential hazards. Properly applying these principles ensures that when explosions occur, they do so with an understanding of their physics, leading to safer and more efficient practices.
In sum, the striking contrast between the conservation of momentum and the often elusive nature of kinetic energy encapsulates the dichotomy of explosions within the realm of physics. Momentum remains a steadfast guardian, preserving the essence of movement, while kinetic energy pirouettes away, transformed and turbulent. As society increasingly grapples with energy conservation and its environmental implications, grasping these principles is vital for both the scientific community and the public at large. Encapsulating the awe of explosions within the steadfast structure of physics provides a unique lens through which to examine our universe, highlighting the delicate balance of energy that defines the world we inhabit.