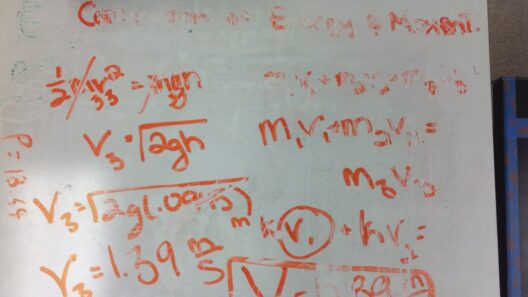The intricacies of physics often beguile even the most astute minds, especially when delving into the realms of momentum and kinetic energy. One might ponder: How can momentum be conserved in a collision while kinetic energy remains unscrupulously altered? This conundrum forms the bedrock of classical mechanics, lending insight into the variances that arise during interactions among particles. As we unravel this concept, it becomes imperative to realize that the conservation of momentum and the conservation of kinetic energy are not interchangeable; rather, they occur under distinct conditions.
To begin with, let’s elucidate the fundamental definitions. Momentum is defined as the product of an object’s mass and its velocity. Mathematically, it is expressed as p = mv, where p denotes momentum, m signifies mass, and v represents velocity. This vector quantity reflects both the magnitude and direction of motion. Conversely, kinetic energy—an expression of the energy of motion—is articulated through the equation KE = ½ mv². Kinetic energy is a scalar quantity, encompassing only magnitude without regard for direction.
Understanding these differences opens a portal into the discussion of collision types—elastic and inelastic collisions. In elastic collisions, both momentum and kinetic energy are conserved. Imagine two billiard balls gently colliding; they bounce off each other, maintaining their total kinetic energy post-collision. This phenomenon occurs during interactions where no energy is dissipated in the forms of heat, sound, or any other energy transformation. The conservation laws in such scenarios stand steadfast.
However, when diving into inelastic collisions, the narrative shifts dramatically. In such interactions, momentum is conserved, but kinetic energy succumbs to transformation. Consider a common example: two vehicles crashing together. Upon impact, the total momentum of the system—comprising both vehicles—remains conserved, yet the kinetic energy dissipates as thermal energy, sound, or deformation occurs in the materials involved. It begs the question: What allows momentum to be stable while energy is susceptible to loss?
The crux of the matter lies in the governing principles that dictate these conservation laws. Momentum conservation stems from Newton’s laws of motion, particularly the second law, which delineates how forces act on masses over time. When two bodies collide, the forces they exert upon one another are equal and opposite, resulting in no net change in their total momentum. This principle pervades all collisions, both elastic and inelastic, underscoring the consistency of momentum conservation.
Kinetic energy, however, is markedly influenced by the nature of the forces at play. During inelastic collisions, some of the kinetic energy is transformed into other forms due to irretrievable processes. The deformation of the colliding bodies—such as crumpling metal in a car crash—represents a sanctuary where that kinetic energy is irreversibly lost to other forms. This surrender indicates that while momentum reigns as an inviolable quantity, kinetic energy is not a stalwart companion. Instead, it is subjected to nature’s whims, morphed and lost in the symphony of collision.
But let’s dissect the implications of these principles further. In scenarios involving perfectly inelastic collisions, where objects stick together post-collision, the transformation of kinetic energy becomes even more pronounced. When two masses coalesce, kinetic energy transformation is palpable—the initial kinetic energy dissipates drastically as the bonded entities share momentum. The momentum before the collision equals the momentum after, yet the collective kinetic energy is diminished. This phenomenon elucidates the fact that energy can neither be created nor destroyed, only transformed.
In contrast, during elastic collisions, the pristine state of the system allows for the restoration of kinetic energy. Herein lies the ability of elastic materials to rebound—a characteristic that universal interactions present in molecular physics. Consider the behavior of high-quality rubber balls, which exemplify elastic collisions remarkably; they return nearly all of their kinetic energy after contact with a surface. Thus, while these two forms of energy can sometimes dance together in harmony, they often diverge, elucidating their distinct natures.
As we spiral into deeper considerations surrounding these phenomena, it’s essential to acknowledge practical repercussions. The universality of momentum conservation underpins myriad applications, from engineering to sports science. In vehicle safety standards, the understanding of momentum conservation is vital for developing crumple zones designed to absorb impact energy effectively. Whereas the conservation of kinetic energy might be idealized in controlled environments, real-world applications necessitate a nuanced understanding of energy losses in collisions.
In conclusion, the disparity between momentum and kinetic energy conservation is a reflection of the underlying physics that governs our universe. Momentum’s steadfastness, juxtaposed with kinetic energy’s susceptibility to transformation, showcases the dynamic interplay of forces during interactions. As we cultivate a deeper comprehension of these principles, we not only augment our scientific knowledge but also illuminate pathways for their application across various fields, paving the way for advancements that harmoniously coexist within the frameworks of engineering, environmental science, and beyond. The dance of momentum and kinetic energy continues, calling upon our intellect to explore further and question even more fervently.