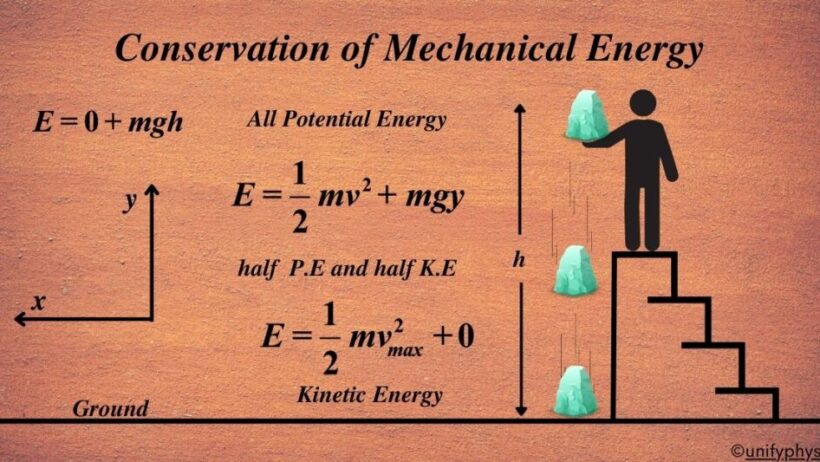
The principle of conservation of mechanical energy is fundamental in physics, intricately linking potential and kinetic energy within an isolated system. This principle holds true that the total mechanical energy in an ideal system remains constant, provided no external forces such as friction act upon it. This observation, while straightforward, encapsulates a multitude of deeper complexities, which evoke enthusiasm among both budding students and seasoned physicists. The allure lies in its application across various domains, from the simplicity of a pendulum swing to the intricate mechanics of roller coasters. By grasping how to calculate conservation of mechanical energy, one delves into an essential aspect of classical mechanics.
Calculating conservation of mechanical energy involves understanding two primary forms of energy: kinetic energy (KE) and potential energy (PE). Kinetic energy pertains to the energy of motion. It is mathematically represented as:
KE = ½ mv²
Here, m denotes the mass of the object and v signifies its velocity. Potential energy, on the other hand, typically refers to gravitational potential energy in this context. It is given by the equation:
PE = mgh
In this equation, g represents the acceleration due to gravity (9.81 m/s² on Earth), and h signifies the height of the object above a reference point. The conservation of mechanical energy states that the sum of kinetic and potential energy in an isolated system remains constant over time. Thus, one can express this conservation principle mathematically as:
KE_initial + PE_initial = KE_final + PE_final
To illustrate this concept, let’s consider a classic physics problem: a ball dropped from a height. At its initial state, when the ball is at rest at the peak height, the kinetic energy (KE_initial) is zero, and the potential energy (PE_initial) is at its maximum, given by:
PE_initial = mgh
As the ball descends, potential energy converts into kinetic energy. When reaching the ground just before impact, the potential energy (PE_final) becomes zero, while the kinetic energy (KE_final) reaches its peak:
KE_final = mgH
This process demonstrates the fluid nature of energy transformation. The beautiful symmetry of energy conservation captivates observers, prompting deeper exploration into the principles governing motion and stability. The continuity of energy flow from one form to another is both an observable phenomenon and a striking principle woven into the fabric of our physical universe.
To perform a conservation of mechanical energy calculation, follow these detailed steps:
Step 1: Identify the Object and Its Parameters
Step 2: Calculate Initial Potential Energy
PE_initial = mgh = 2 kg × 9.81 m/s² × 10 m = 196.2 J
This calculation reveals the initial potential energy of the ball when it is at rest, emphasizing the energy stored due to its elevated position.
Step 3: Assess Initial Kinetic Energy
KE_initial = ½ mv² = ½ × 2 kg × (0 m/s)² = 0 J
Step 4: Determine Final States of Energy
PE_final = 0 J
Now calculate the final kinetic energy just before impact. Since the ball reaches the ground, all energy converts into kinetic energy:
KE_final = PE_initial = 196.2 J
Step 5: Verify Conservation of Energy
KE_initial + PE_initial = KE_final + PE_final
0 J + 196.2 J = 196.2 J + 0 J
This equality confirms the principle of conservation of mechanical energy. The total energy remains constant throughout the object’s motion, underscoring the intricate balance of energy forms.
In closing, the capability to calculate conservation of mechanical energy reveals the dance between kinetic and potential energy. This dynamic interplay not only empowers scientific inquiry but also deepens our appreciation for the laws governing motion. The fascination with energy conservation transcends mere academic pursuit; it invites inquiry into the underlying mechanics of everyday phenomena and fosters a broader understanding of our environment. As we engage with these principles, we open pathways for innovative applications across technological advances and ecological considerations, underscoring the significance of this fundamental concept in both physics and environmental stewardship.