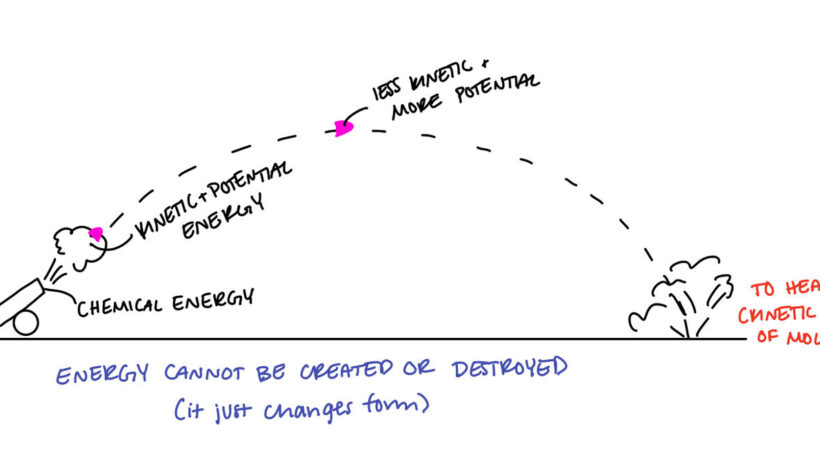
Understanding the conservation of energy is pivotal in solving numerous physics problems. At its core, the principle asserts that energy cannot be created or destroyed, only transformed from one form to another. This constant underpins many natural phenomena and allows us to predict the behavior of objects in motion, among other scenarios. Yet, knowing when to apply this principle can be perplexing, particularly when confronted with various physical systems. Here, we will delve into the nuances of the conservation of energy, equipping you with the insight needed to approach related problems with confidence and clarity.
First, it is paramount to recognize the various forms energy can take. Kinetic energy, the energy of motion, is what propels objects and results from their velocity. Potential energy, on the other hand, is stored energy derived from an object’s position or state. Gravitational potential energy, for example, depends on an object’s height above the Earth’s surface, suggesting that the higher an object is positioned, the more potential energy it possesses. The interplay between these energy types is crucial, particularly in a closed system where external forces are negligible.
Identifying a closed system is the first step in determining whether to use the conservation of energy principle. A closed system is characterized by energy exchanges that do not involve outside forces. For instance, consider a swinging pendulum. As it ascends, kinetic energy is transformed into gravitational potential energy until the peak of a swing, where it momentarily halts. Upon descending, that potential energy is converted back into kinetic energy. Throughout this motion, the total energy remains constant, adhering to the conservation of energy principle. Thus, a system is primed for energy conservation analysis when no external work is done, and friction or other dissipative forces are negligible.
However, not every problem lends itself to this principle seamlessly. The presence of non-conservative forces, such as friction or air resistance, complicates the scenario considerably. In cases where energy is lost to heat or sound due to friction, the conservation of energy principle must be modified. The total mechanical energy of the system decreases over time, revealing that energy is being transformed into forms that do not contribute to the mechanical work done by the system. A classic example is a sliding block coming to rest after traveling along a rough surface; the friction converts kinetic energy into thermal energy, showcasing that loss must be accounted for in calculations.
Furthermore, in problems involving springs or elastic potential energy, one must also be vigilant about the potential energy stored when the spring is compressed or extended. The energy conservation equation takes the form of kinetic plus potential energy, encompassing both gravitational and elastic potential energy. When analyzing such problems, ensure that you account for all forms of energy in the initial and final states of the system.
Transitioning to scenarios involving multiple objects or systems can heighten complexity. In perfectly isolated interactions—like collisions between two billiard balls—energy conservation plays a crucial role. For elastic collisions, both kinetic energy and momentum are conserved, while in inelastic collisions, momentum is conserved but kinetic energy is not. Distinguishing between these types of collisions is vital, particularly when approaching problems in kinematics and dynamics. Understanding what allows for global energy conservation versus local interactions can dramatically shift one’s approach to problem-solving.
Equally important is the application of energy conservation in rotational motion. When an object rotates, both translational and rotational forms of kinetic energy must be considered. Here, the moment of inertia, a measure of an object’s resistance to change in rotation, becomes critical. If analyzing a spinning disk or wheel, one must compute both types of kinetic energy to ascertain overall conservation states during interactions, such as rolling or sliding.
To further hone your analytical skills, engaging in practice problems that vary in context will truly illuminate when energy conservation can be applied. Utilizing scenarios from practical situations—such as roller coasters, planetary motion, or even electrical circuits—enhances your comprehension. It also cultivates an intuitive grasp of energy transformation, enabling you to recognize patterns and apply the principle with ease.
For instance, envision a roller coaster ascend a hill. Analyzing this system, potential energy reaches its zenith at the apex, while kinetic energy is maximized during the descent. Alternatively, should you examine a pendulum’s arc, oscillations reveal energy transformation between potential and kinetic realms. Each situation is an invitation to explore the interplay of energy, encouraging curiosity and critical thinking.
In closing, mastering the application of energy conservation involves meticulous identification of system boundaries, forms of energy present, and external forces at play. The decision to invoke this principle depends on recognizing a closed system, understanding energy losses, and appreciating the context of the problem. Delving deeper into these principles not only sharpens problem-solving acumen but also offers a rewarding perspective on the interconnectedness of energy in our universe. This newfound perspective can transform your approach to physics, bridging theoretical concepts with real-world phenomena.
By cultivating a rigorous understanding of these concepts, you position yourself to approach physics problems with greater confidence, shaped by the elegance of energy conservation. The equations underlying energy conservation are but a tool; it is the application of this understanding that opens doors to a broader curiosity about the natural world.