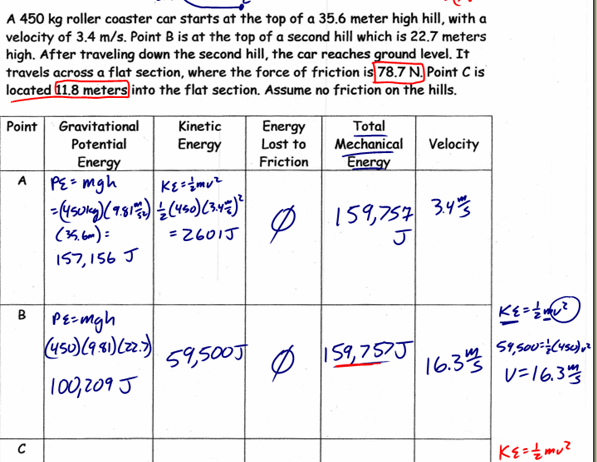
In the realm of physics, the conservation of mechanical energy is a foundational principle that posits that in the absence of non-conservative forces, the total mechanical energy of an isolated system remains constant. This principle is instrumental when analyzing various physical situations, including those involving friction, a ubiquitous and often neglected force in many theoretical calculations. Understanding how to account for the role of friction is critical not only for accurately predicting the behavior of systems but also for fostering a profound comprehension of energy dynamics in our everyday lives.
To begin, let us clarify what we mean by mechanical energy. Mechanical energy is generally defined as the sum of kinetic energy (the energy of motion) and potential energy (the energy stored due to position). In ideal situations, where friction and other non-conservative forces are absent, the mechanical energy of a system remains constant. However, the introduction of friction disrupts this harmonious balance, leading us to reevaluate our calculations and conceptualizations of energy transfer.
Friction arises from the interactions between the surfaces of objects in contact. It is omnipresent, albeit sometimes subtle, and manifests as resistance to motion. Understanding the nature of friction is imperative when applying conservation principles. There are two principal types of friction: static friction, which prevents motion from initiating, and kinetic friction, which acts on moving objects. Both forms dissipate mechanical energy, converting it into thermal energy, hence complicating the conservation narrative.
When analyzing a system under the influence of friction, the first step is to model the frictional force accurately. The frictional force can be expressed as:
Ff = μFN
Here, μ is the coefficient of friction (a dimensionless scalar) that depends on the materials in contact, and FN is the normal force acting on the object. The coefficient of friction must be determined experimentally, as it varies with surface texture, temperature, and the presence of lubricants.
Once the frictional force is understood, one must consider how this force affects the total work done on the system. The work done by friction is a non-conservative force and is given by:
Wf = -Ff × d
Where d is the distance over which the force is applied. The negative sign indicates that friction opposes the motion of the object. The work done by friction results in a reduction of the system’s mechanical energy, leading to an equation that illustrates the energy transformation:
ΔE = ΔKE + ΔPE + Wf
In this context, ΔE represents the overall change in mechanical energy, ΔKE is the change in kinetic energy, and ΔPE denotes the change in potential energy. Since work done by friction is dissipative in nature, it serves as a critical component of energy transfer calculations.
Now, let us delve into practical applications to illustrate how these principles manifest in a tangible way. Consider a simple system of a block sliding down an inclined plane. In the absence of friction, one can easily apply the conservation of mechanical energy to determine how high the block descends or its final velocity at the bottom. Yet, when friction is introduced, the analysis becomes significantly more complex. The mechanical energy of the system is no longer conserved; some energy has transformed into heat due to friction, which means careful consideration must be given to the frictional forces at work.
Quantifying the energy loss due to friction not only aids in achieving accurate results but also enhances practical engineering applications. For example, in the design of vehicles, engineers must account for frictional forces to optimize fuel efficiency. Similarly, understanding energy losses in machinery is paramount for improving performance and sustainability.
Moreover, addressing friction is not merely a matter of theoretical curiosity; it is intrinsically linked to broader environmental considerations. As we strive for greater efficiency and sustainability in our energy systems, understanding how energy is converted, dissipated, and conserved becomes increasingly critical. Incorporating friction into energy calculations allows for the identification of opportunities to minimize energy loss in various applications, thereby reducing our carbon footprint.
In conclusion, the conservation of mechanical energy in systems affected by friction represents a nuanced interplay between forces, energy transfer, and practical application. Accurately accounting for the dissipative nature of friction is essential for obtaining realistic insights and developing effective strategies for energy management. As we navigate the complexities of energy dynamics, embracing the intricacies of friction not only fosters scientific understanding but also propels us toward a more sustainable future. In a world increasingly aware of the implications of energy usage on climate change, such knowledge is of paramount importance, bridging the gap between theoretical physics and environmental stewardship.