Understanding the principles behind the conservation of energy is fundamental in the field of physics. This principle dictates that energy cannot be created or destroyed, but can only be transformed from one form to another. In this comprehensive guide, we will delve into the methodologies for calculating conservation of energy, elucidating the various forms and scenarios where this principle is applicable.
First and foremost, it is crucial to familiarize oneself with the different types of energy. The primary categories include kinetic energy, potential energy, thermal energy, and elastic energy, among others. Kinetic energy, expressed mathematically as KE = 1/2 mv² (where m represents mass and v denotes velocity), reflects the energy possessed by an object due to its motion. Potential energy, on the other hand, is associated with an object’s position or configuration. The most common form is gravitational potential energy (PE), which can be calculated using the formula PE = mgh, where h is the height above a reference point and g is the acceleration due to gravity, approximately 9.81 m/s² on Earth.
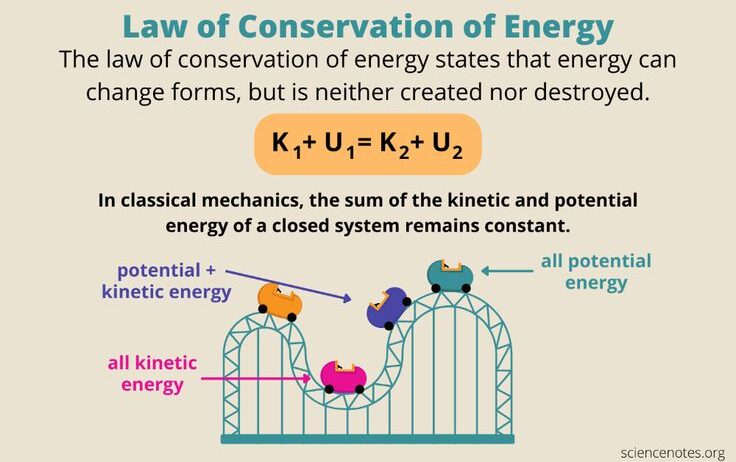
The law of conservation of energy posits that the total energy within a closed system remains constant. For example, when a ball is thrown upwards, it possesses high kinetic energy at the moment of release. As it ascends, kinetic energy is converted into potential energy until it reaches its apex. At this point, the ball has maximum potential energy and zero kinetic energy. As it descends, this potential energy is once again converted to kinetic energy. To calculate the energy at different points, observe that the total energy (initial kinetic + initial potential) remains equal to the total energy at the peak and during the descent:
Initial energy = Kinetic energy at launch + Potential energy at launch
Final energy = Kinetic energy at peak + Potential energy at peak.
To apply this in a practical calculation, consider a scenario where a ball of mass 2 kg is thrown with an initial velocity of 10 m/s. The initial kinetic energy can be calculated:
KE_initial = 1/2 mv² = 1/2 (2 kg)(10 m/s)² = 100 J.
Assuming the ball is thrown from a height of 0 meters, its initial potential energy is zero. Thus, the total energy at launch is:
Total energy = KE_initial + PE_initial = 100 J + 0 J = 100 J.
At its maximum height, let’s assume the ball reaches 5 meters. Its potential energy can now be recalculated as:
PE = mgh = (2 kg)(9.81 m/s²)(5 m) = 98.1 J.
Since total energy is conserved, the kinetic energy at the peak height can be determined by:
KE_peak = Total energy – PE_peak = 100 J – 98.1 J = 1.9 J.
This example illustrates the transformation of energy as predicted by the conservation law. By practicing such calculations, one becomes adept in recognizing the energy transitions occurring in various physical contexts.
Another area to explore is the concept of mechanical energy, which is the sum of kinetic and potential energy in a system. Mechanical energy conservation applies in situations where only conservative forces are doing work, such as gravity and spring forces. In scenarios involving friction or air resistance, energy is still conserved; however, some energy is dissipated as thermal energy, complicating the straightforward application of conservation calculations.
Beyond classical mechanics, the conservation of energy also plays a pivotal role in thermodynamics. Thermal energy, related to the kinetic energy of particles, brings forth a unique aspect of energy conservation where heat exchanges occur. The First Law of Thermodynamics asserts that the change in internal energy of a system equals the heat added to the system minus the work done by the system:
ΔU = Q – W.
In practical applications involving heat engines, understanding energy conservation is essential for efficiency calculations. By determining the ratios of useful energy output to energy input, one can assess the performance of these systems.
Moreover, advancements in renewable energy technologies further necessitate a profound appreciation for energy conservation principles. For instance, in solar energy systems, understanding how solar energy converts into electrical energy encapsulates a real-world application of conservation laws. By analyzing the efficiency of photovoltaic cells, engineers employ conservation principles to enhance energy capture and utilization, resonating with the increasing global focus on sustainability.
Lastly, modern developments in energy conservation extend to the assessment of energy in non-mechanical systems. This encompasses areas like nuclear physics, where the binding energy of nucleons is a critical factor for understanding nuclear fission and fusion processes. The mass-energy equivalence principle, articulated by Einstein’s equation E=mc², enunciates that mass can be converted into energy, providing a profound insight into conservation in high-energy contexts.
In conclusion, mastering the calculation of conservation of energy necessitates a profound comprehension of not only the basic equations of kinetic and potential energies but also a broader perspective on how these principles interact with various forms of energy in different contexts. Through diligent practice and application of these principles, one can navigate the intricacies of energy transformations, illuminating the path toward greater understanding and innovation in physics.