Have you ever gazed up at the stars and wondered how spacecraft manage to escape Earth’s pull? What if I told you that there’s a fascinating interplay of physics at work here, specifically involving escape velocity? The concept integrates principles from both kinematics and thermodynamics, forming a cornerstone of astrophysics. Understanding escape velocity through the lens of conservation of energy creates a pathway to appreciate how vehicles overcome gravitational forces. So how exactly is escape velocity quantified? Let’s dive into the intricacies of this compelling subject.
At its essence, escape velocity is the minimum speed an object needs to reach in order to break free from a celestial body’s gravitational grasp without additional propulsion. The formula is simple and elegant, yet the implications of understanding it are profound. The foundational approach utilizes conservation of energy—the principle that energy is neither created nor destroyed but transformed from one form to another. This means that the total mechanical energy of a system remains constant, assuming no non-conservative forces like friction act upon it.
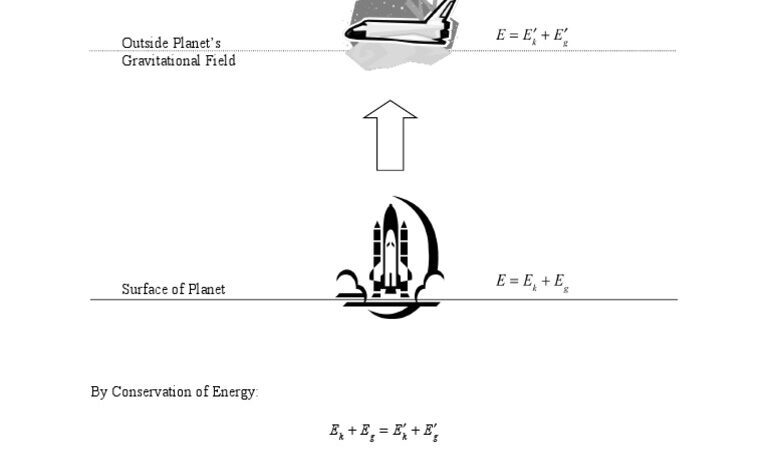
To elaborate, consider the total mechanical energy (E) of a body under the influence of gravity. This energy comprises two components: kinetic energy (KE) and gravitational potential energy (PE). Kinetic energy is given by the formula: KE = 0.5 * m * v², where m is mass and v is velocity. Gravitational potential energy can be expressed as: PE = – (G * M * m) / r, where G is the gravitational constant, M is the mass of the celestial body, m is the mass of the object attempting to escape, and r is the distance from the center of the celestial body.
When an object reaches escape velocity, its total mechanical energy becomes zero at an infinite distance from the planet, where both kinetic and potential energies balance out. Therefore, we can establish the equation: KE + PE = 0. This translates to: 0.5 * m * v² – (G * M * m) / r = 0. Simplifying this equation leads us to the pivotal moment where we isolate escape velocity (ve):
ve = sqrt((2 * G * M) / r)
Here, it’s crucial to grasp each variable’s significance. The mass of the celestial body (M) profoundly affects the escape velocity. The more massive the body, the stronger the gravitational pull, and the higher the escape velocity required. For instance, the escape velocity of Earth is approximately 11.2 kilometers per second. In contrast, the Moon, which has substantially less mass, has an escape velocity of about 2.4 kilometers per second.
Similarly, distance from the center of the celestial body plays a paramount role. The further an object is from the center, the smaller the gravitational force acting upon it. For example, a spacecraft launched from a high altitude would need less velocity to escape Earth’s gravity compared to one launched from sea level. This principle can be observed through orbital mechanics. The trajectory of an object in orbit follows a delicate equilibrium between gravitational pull and centrifugal force, a beautiful dance dictated by energy conservation.
This leads us to an intriguing challenge: consider a scenario where a projectile is launched vertically into space. Imagine you have the opportunity to launch a small satellite into orbit. You may ask, what happens when the velocity of the satellite falls below the escape velocity? The satellite would eventually descend back to Earth, impacted by the force of gravity. However, by employing the right launch parameters, the satellite could be placed in a stable orbit, continuously falling toward Earth while also moving forward, akin to how the Moon orbits our planet.
In practice, engineers and scientists utilize simulation models obtained through high-level computational mechanics to determine the viability of escape. They must consider various factors, such as atmospheric drag, fuel consumption, and structural integrity, to ensure that a spacecraft adheres to the theoretical escape velocity. Thus, calculating escape velocity is not just a theoretical exercise—it translates into real-world applications that bridge science and engineering.
Moreover, conservation of energy principles play a pivotal role in enhancing our understanding of not just escape velocity but also celestial mechanics and orbital dynamics. The universe is a complex system where energy transformations govern the motion of celestial objects. Comprehending escape velocity illuminates grander concepts such as orbital transfers, collisions, and even the dynamics of galaxies.
In conclusion, establishing the escape velocity using conservation of energy principles reveals an enduring truth about the universe: the interconnectedness of forces and energies. By amalgamating intricate calculations with profound scientific understanding, we unravel the mechanics that govern not only space travel but also the fabric of existence itself. As we ponder our capabilities for exploration, remember the energy preserved and transformed on the journey into the cosmos. While astronauts may soon traverse the limits of our atmosphere, each mission is a testament to the tireless pursuit of knowledge that drives humanity forward.