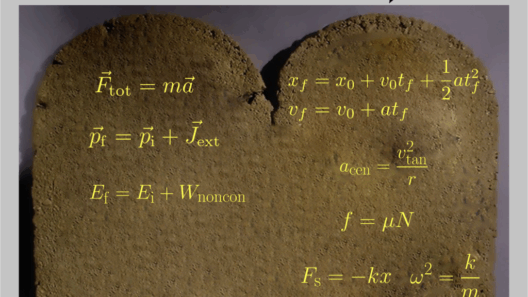The force of friction is a fundamental omnipresence within the realm of physics, acting as a resistant force that opposes the motion of objects in contact. When examining this fascinating phenomenon, one discovers a rich interplay between various physical principles, most notably the conservation of energy. This guide elucidates how to calculate the force of friction while contextualizing it through the lens of energy principles.
Friction arises from the microscopic interactions between two surfaces. At the macroscopic level, it can be perceived as a continuous struggle between surfaces that possess irregularities at the atomic level. This innate roughness causes the surfaces to exert forces upon one another, thus creating resistance. The significance of this force cannot be overstated, as it is crucial in both natural and engineered systems, influencing everything from the simple act of walking to the complex dynamics of vehicular travel.
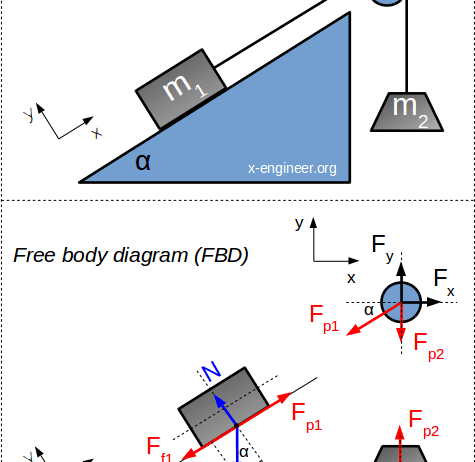
To delve deeper into the calculation of the force of friction, one must first familiarize oneself with the two primary types: static friction and kinetic friction. Static friction acts when two objects are at rest relative to each other, while kinetic friction comes into play when these objects are sliding past one another. These distinct categories are often governed by the coefficient of friction, a dimensionless value that characterizes the frictional properties between specific materials.
The basic formula for calculating the frictional force (F_friction) can be expressed as:
F_friction = μ * N
Here, μ represents the coefficient of friction, while N denotes the normal force—the perpendicular force exerted by a surface against an object resting upon it. The coefficient of friction is not a universal constant; it varies depending on the materials in contact. For instance, rubber on concrete exhibits a higher coefficient of friction than ice on metal, directly impacting the magnitude of frictional force in various scenarios.
Normal force, N, can be nuanced in its calculation. If an object is placed on a flat surface, N is typically equal to the object’s weight, which is given by the equation:
N = m * g
In this equation, m represents the mass of the object, and g is the acceleration due to gravity (approximately 9.81 m/s² on Earth). If the surface is inclined, the normal force must be adjusted based on the angle of the incline (θ). This can complicate matters, as the relationship between the forces acting on the object becomes slightly intricate:
N = m * g * cos(θ)
Understanding these forces and how they interact is vital when applying the conservation of energy principles. The conservation of energy postulates that energy can neither be created nor destroyed; it can, however, be transformed from one form to another. In scenarios involving friction, kinetic energy may be converted into thermal energy or potential energy may be dissipated through work done against friction.
Let’s illustrate this concept further through a simple example: a block sliding down an inclined plane. As the block descends, it possesses gravitational potential energy, which, in the absence of friction, would convert directly into kinetic energy. However, the presence of friction alters this exchange. The force of friction acts against the motion of the block, converting some of the gravitational potential energy into thermal energy due to the inherent interactions at the surface level.
This relationship between energy forms highlights an essential aspect of mechanical systems. Knowing the frictional force acting upon an object allows for the prediction of its deceleration and the amount of energy lost to friction. The work done against friction (W_friction) can be calculated using the equation:
W_friction = F_friction * d
Where d is the distance over which the force is applied. This work done against friction ultimately translates into thermal energy, dissipated into the environment, reinforcing the significance of understanding friction in both natural phenomena and engineered applications.
Exploring the implications of friction leads to further fascination. In many cases, optimizing friction can yield significant benefits. For instance, in engineering applications, careful selection of materials can minimize friction in machinery, translating to reduced energy costs and enhanced efficiency. Alternatively, in the realm of sustainability, understanding friction can inform the development of eco-friendly transport systems and energy-efficient vehicles.
Taking a step back, one can appreciate how the principles of friction and conservation of energy interplay to create a symphony of motion across various systems. Life is replete with examples: the friction that enables a car to brake, the resistance felt when walking on different surfaces, or the struggle of ice skates gliding on a rink—all illustrate a convergence of physical laws in action.
Moreover, the broader implications of these principles extend beyond the realm of physics into environmental considerations. The frictional force, often overlooked, plays a role in addressing climate change. By understanding how energy dissipates in mechanical systems, engineers and scientists can design more efficient systems that minimize energy loss and reduce carbon footprints. This interconnectedness highlights the need for an interdisciplinary approach as humanity grapples with environmental challenges.
In summation, calculating the force of friction is a fundamental endeavor that reveals deeper insights into energy dynamics. The interplay of static and kinetic friction, the variables that impact the coefficient of friction, and the implications of these forces underscore a captivating journey through the principles of physics. As we seek to harness this knowledge, we open pathways to innovative solutions for a sustainable future.