The principle of conservation of energy is an enduring concept that permeates numerous scientific disciplines, especially physics. This foundational law posits that energy cannot be created or destroyed; it can only change forms. To derive the conservation of energy systematically, one must traverse several fundamental concepts and principles of mechanics. By doing so, we uncover not only the mechanics involved but also the underlying philosophy that captures the imagination of thinkers and scientists alike.
To begin with, consider a closed system: a pool table, for instance, where balls interact without friction or external influence. When a cue strikes a ball, the kinetic energy of the cue transforms into the kinetic energy of the struck ball. Initially, the energy exists as the motion of the cue, but upon impact, it gets transferred and reconfigured. The laws governing these interactions can be delineated through the lens of Newtonian mechanics.
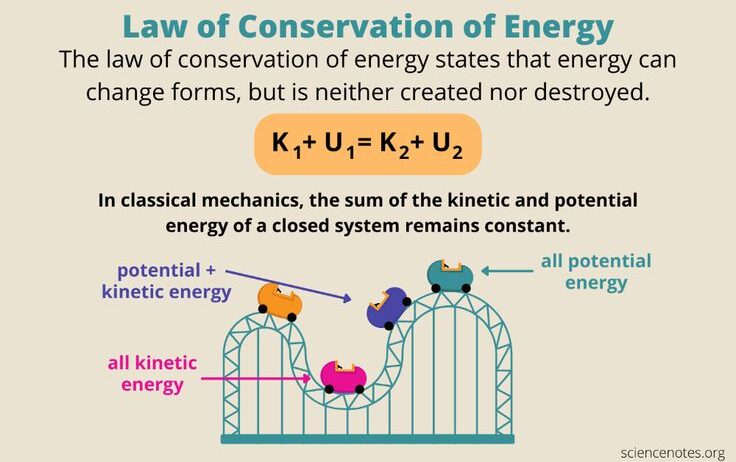
The first step in deriving conservation of energy is by selecting a closed system devoid of external forces. This restriction is crucial as it allows for an isolated analysis where energy can neither dissipate nor accumulate from outside sources. In an ideal scenario, the sum of kinetic and potential energies remains constant. The equations of motion, embodied in the kinematic equations, will be instrumental as we elucidate this conservation law.
Now, let’s discuss kinetic energy (KE), which is mathematically expressed as KE = (1/2)mv², where ‘m’ denotes mass, and ‘v’ represents velocity. When an object moves, it accumulates kinetic energy proportional to its velocity squared. The faster the object moves, the more kinetic energy it possesses. Conversely, gravitational potential energy (PE), represented as PE = mgh (where ‘g’ is gravitational acceleration and ‘h’ is height above a reference point), captures the energy stored in an object’s position within a gravitational field.
To observe the interplay of kinetic and potential energy, consider a pendulum. At its maximum height, the pendulum possesses maximum potential energy, but as it swings down to its lowest point, that potential energy is converted into kinetic energy. At the midpoint, the potential energy is minimal, while kinetic energy reaches its maximum. This fluctuation between energy forms exemplifies the fluidity of energy conservation.
Mathematically, this phenomenon can be represented as follows:
PE_initial + KE_initial = PE_final + KE_final
Substituting the expressions for potential and kinetic energy produces:
mgh_initial + (1/2)mv_initial² = mgh_final + (1/2)mv_final²
This equation, known as the energy conservation equation, illustrates that the total mechanical energy remains constant in the absence of non-conservative forces, such as friction or air resistance. Hence, this leads us into the next consideration—non-conservative forces.
When non-conservative forces are at play, such as friction, the behavior of energy within a system becomes notably complex. These forces convert mechanical energy into thermal energy, dissipating it into the environment. Consequently, in a real-world scenario involving a sliding object, the energy is not conserved in its mechanical form alone. Here, the energy transformation must take into account loss due to friction.
To incorporate these forces, we adjust our fundamental equation:
ΔE = W_non-conservative
Where ΔE represents the change in mechanical energy and W_non-conservative signifies the work done by non-conservative forces. This refinement highlights how energy can transition not just between kinetic and potential forms but also into less usable forms due to wasteful processes.
Moving forward, it is essential to explore the ramifications of conservation of energy beyond simple mechanical systems. In thermodynamics, for instance, energy conservation applies to heat exchanges and thermodynamic cycles, such as the Carnot cycle. The principles that govern these transitions illustrate that energy, regardless of its form, always adheres to the conservation principle.
In contemporary physics, the conservation of energy extends into realms such as electromagnetism and relativity. For example, in electromagnetic systems, the interplay between electric and magnetic fields manifest energy conservation through the Poynting vector. Through understanding these systems, the multifaceted mechanisms of energy transfer become evident, revealing the interconnectedness of physical laws.
Philosophically, the conservation of energy stands as a testament to the predictability and constancy of natural laws. It embodies a fundamental truth that resonates not only in scientific inquiry but also in broader philosophical discourse. This equilibrium propels our understanding of the universe, evoking a sense of wonder. The intricate dance of energy forms—the oscillation between potential and kinetic energy—mirrors a more profound order that governs all matter and motion.
In conclusion, deriving the conservation of energy is not merely an academic exercise but a journey into the very fabric of reality. From simple mechanical systems to complex interactions in advanced physical concepts, the law remains a cornerstone that underpins diverse fields of study. Recognizing its implications fosters a greater appreciation for the interconnectedness of forces at play in our universe, suggesting that energy, in its many forms, is a primary currency of the cosmos, forever transforming, yet eternally constant.