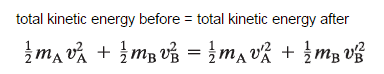In the realm of physics, the law of conservation of mechanical energy serves as a cornerstone principle. It asserts that within a closed system, the total mechanical energy remains constant, provided that no external forces perform work on the system. Imagine the conservation of mechanical energy as a perfectly balanced teeter-totter. One side rises when the other descends, maintaining equilibrium. This article elucidates the methodology to ascertain if mechanical energy is conserved, guiding you through a systematic approach that unravels this fundamental concept.
Understanding Mechanical Energy
Before embarking on this investigative journey, it is imperative to grasp the two primary components of mechanical energy: kinetic energy (KE) and potential energy (PE). Kinetic energy is the energy of motion, quantified by the equation KE = ½ mv², where m represents mass and v denotes velocity. In contrast, potential energy is the energy stored in an object due to its position or configuration. For gravitational potential energy near the Earth’s surface, the equation PE = mgh is employed, with g representing acceleration due to gravity and h indicating height above a reference point.
The Step-by-Step Approach
To determine whether mechanical energy is conserved, follow these methodical steps:
Step 1: Define the System
The first step involves delineating the boundaries of your system. Are you observing a roller coaster’s ascent and descent, or perhaps a pendulum’s swing? By clearly establishing the limits of your system, you can effectively isolate the internal forces at play. This delineation helps to avoid extraneous variables, akin to drawing a circle in the sand to mark your territory in the realm of physics.
Step 2: Identify the Forces Involved
Next, evaluate the forces acting within your defined system. In the case of the pendulum, gravity is a predominant force. However, if friction or air resistance plays a role, these dissipative forces can detract from mechanical energy, much like how the persistent drizzle can slowly erode a beautiful landscape. Understanding these forces is crucial, as they dictate the energy exchanges that occur.
Step 3: Calculate Initial and Final Mechanical Energy
Proceed to calculate both the initial and final mechanical energy for your system. The mechanical energy at any point is the sum of kinetic and potential energy. To begin, gather relevant data: measure the mass, velocity, and height of your object. Employ the formulas for KE and PE to calculate the initial mechanical energy (E_initial) and the final mechanical energy (E_final) at critical points in the motion. Think of this process as conducting a balance sheet for energy assets. If E_initial = E_final, then mechanical energy is conserved.
Step 4: Identify Energy Losses
Should the initial and final energies not equate, delve into the energy loss mechanisms. Assess whether non-conservative forces, such as friction, thermal energy loss, or deformation, have siphoned off energy from the system. This analysis is akin to investigating a leaky bucket—if the bucket has holes, the water (in this case, energy) will escape. It is essential to account for these losses when evaluating the total mechanical energy.
Step 5: Verify Conditions for Conservation
For mechanical energy to remain conserved, the system must be isolated from external work. Ensure there are no other forces actively contributing to energy exchanges. This evaluation mirrors the scrutiny an artist applies when ensuring no extraneous colors blur their masterpiece. If external work is absent, and the only forces at play are conservative—such as gravitational forces—then mechanical energy conservation prevails.
Real-World Applications
Understanding the conservation of mechanical energy has profound implications in both theoretical and applied physics. For instance, roller coasters utilize this principle to ensure thrilling rides while minimizing energy expenditure. Pendulums demonstrate energy transformation elegantly: as they swing, potential energy at their peaks converts to kinetic energy at their lowest points. Such applications resonate throughout engineering solutions, energy conservation strategies, and even the design of sustainable systems in an era increasingly challenged by climate change.
Conclusion
In summation, determining whether mechanical energy is conserved requires a thoughtful investigation rooted in systematic analysis. By defining your system, identifying forces, calculating energy states, recognizing energy losses, and verifying the presence of non-conservative forces, the enchanting world of mechanical energy conservation unfolds before you. As you probe deeper into this fundamental principle, you will realize that energy is not simply a number but an intricate tapestry woven dynamically into the very fabric of our universe.