Conservation of energy is a fundamental concept in physics, underscoring the idea that energy cannot be created or destroyed; it can only change forms. This principle serves as a cornerstone for numerous problem-solving scenarios within the realm of physics education. Mastering conservation of energy problems can seem daunting for students, but with systematic strategies and approaches, success is attainable. This article delineates effective tips and tricks for tackling these problems, enabling learners to enhance their understanding and application of this crucial scientific concept.
Understanding the basic prerequisites for solving conservation of energy problems is imperative. Familiarity with kinetic energy (KE), potential energy (PE), and the work-energy theorem lays the groundwork for deeper exploration. Kinetic energy, defined as the energy an object possesses due to its motion, is calculated with the formula KE = 1/2 mv², where m is mass and v is velocity. In contrast, potential energy, particularly gravitational potential energy, pertains to the energy held by an object due to its position in a gravitational field, formulated as PE = mgh, where g represents the acceleration due to gravity and h signifies height above a reference point.
The first step in approaching conservation of energy problems is to identify the system in question. This involves determining the objects involved and the types of energy present. Once the system is defined, the next crucial phase is to establish the initial conditions and the final conditions of the system. Assess the energy types at the outset—this could include both kinetic and potential energy components—along with the energies present at the conclusion of the problem. This initial assessment creates a framework for subsequent calculations.
In many cases, applying the Law of Conservation of Energy can simplify the process. The law states that the total mechanical energy (the sum of kinetic and potential energy) of a closed system remains constant. Mathematically, it can be expressed as:
KE_initial + PE_initial = KE_final + PE_final.
In practice, this equation will guide your calculations by enabling you to solve for unknown variables. For example, if you know the height of an object and its mass, you can calculate its potential energy. Similarly, if you ascertain the object’s speed, its kinetic energy can be determined as well. The adept use of this equation often illuminates the relationships between the different forms of energy and can be manipulated to isolate and solve for the desired variable.
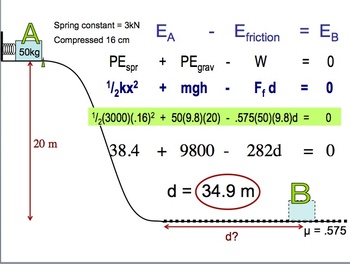
Another essential strategy is the adept move of drawing diagrams. A visual representation can significantly enhance one’s understanding of the problem. Begin with a labeled sketch of the scenario, illustrating all forces, energy types, and known quantities. This practice not only aids in visualizing the energy transformations but can also clarify the relationships between the forces acting on the system. Use arrows to denote movement, and indicate energy transfer points. Diagrams are not merely supplementary; they often elucidate concepts that written equations may obscure.
Practical examples amplify theory into comprehensive understanding. Consider the quintessential example of a roller coaster: as the coaster ascends, mechanical energy transforms into gravitational potential energy. At the peak, potential energy is maximized, and kinetic energy is minimized. As the coaster descends, potential energy dissipates while kinetic energy surges. Serially analyzing such real-world applications can solidify comprehension of principles of energy conservation.
Another key element involves recognizing non-conservative forces, such as friction or air resistance. While conventional conservation of energy equations operate under ideal, frictionless conditions, real-world scenarios often present complexities that must be accounted for. The work done against non-conservative forces results in energy dissipation, usually increasing the complexity of calculations. Understanding the impact of these forces is pivotal for accurately reflecting energy conservation in practical situations. This awareness cultivates adaptability in problem-solving, allowing learners to adjust their strategies based on the context of the scenarios presented.
Additionally, consistent practice is fundamental. Engaging with varied problems—from straightforward numeric calculations to complex application scenarios—fortifies analytical dexterity. Educational resources such as physics textbooks, online platforms, and problem sets often contain a plethora of exercises ideal for honing these skills. Regular practice enables students to recognize patterns, solidify methods, and build confidence in their capabilities.
Moreover, collaborative learning extends beyond individual study methods. Engaging with peers during problem-solving sessions can facilitate collective brainpower and encourage diverse approaches to analysis. Different perspectives often illuminate novel pathways to problem-solving, enhancing understanding through dialogue and discussion.
Supplementary tools and resources can also enhance the learning experience. Interactive simulations that visualize energy transformations and conservation principles can be tremendously beneficial. These digital resources allow learners to manipulate variables and observe immediate results, fostering an intuitive grasp of the concepts.
In summary, tackling conservation of energy problems requires a multifaceted approach involving fundamental principles, effective strategies, and practical applications. By delineating the system, employing the law of conservation of energy, utilizing diagrams, and embracing real-world examples, one builds a robust foundation for success. Recognizing the impact of external forces, maintaining a practice regimen, and engaging collaboratively also contribute significantly to mastering this crucial aspect of physics. With these strategies, students can not only navigate conservation of energy problems successfully but develop an appreciation for the intricate workings of energy in our world.